Question

【题目】已知动圆与圆外切，与圆内切.

（Ⅰ）试求动圆圆心的轨迹的方程；

（Ⅱ）与圆相切的直线与轨迹交于两点，若直线的斜率成等比数列，试求直线的方程；

Answer 1

【答案】（1）（2）或.

【解析】【试题分析】（１）借助两圆的位置关系与半径之间的数量关系建立方程求解；（２）运用直线与椭圆的位置关系建立方程组，通过坐标之间的关系求解：

（Ⅰ）圆可化为，圆可化为，

设动圆的半径为，两定圆的圆心分别为， ，则，

，∴，根据椭圆的定义可知，轨迹是以为焦点的椭圆，且， ，则，

故轨迹的方程为.

（Ⅱ）由题意知直线的斜率存在且不为.

设直线的方程为，

联立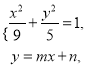

消去得，

设， ，则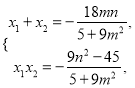

根据直线的斜率成等比数列，

可知，即，

∵，

∴，∴，∴，

由直线与圆相切可得，可得，

故所求直线方程为或.