题目内容
已知向量 ,
, 满足|
满足| |=1,|
|=1,| |=2,
|=2, 与
与 的夹角为60°,向量
的夹角为60°,向量 =2
=2 +
+ .
.
(1)求 的模;
的模;
(2)若向量 =m
=m -
- ,
, ∥
∥ ,求实数m的值.
,求实数m的值.
解:(1)| |2=(2
|2=(2 +
+ )2 =4
)2 =4 2 +4
2 +4 •
• +
+ 2 =4+4×1×2×cos60°+4=12,
2 =4+4×1×2×cos60°+4=12,
故 .
.
(2)因为 ∥
∥ ,
,
所以存在实数λ,使 =λ
=λ ,即 m
,即 m -
- =λ(2
=λ(2 +
+ ).
).
又 ,
, 不共线,
不共线,
所以2λ=m,λ=-1,
解得m=-2.
分析:(1)根据)| |2=(2
|2=(2 +
+ )2 =4
)2 =4 2 +4
2 +4 •
• +
+ 2 ,以及|
2 ,以及| |=1,|
|=1,| |=2,求出|
|=2,求出| |2的值,即可得到
|2的值,即可得到 的模.
的模.
(2)有题意知 存在实数λ,使 =λ
=λ ,即 m
,即 m -
- =λ(2
=λ(2 +
+ ),可得 2λ=m,λ=-1,由此求得实数m的值.
),可得 2λ=m,λ=-1,由此求得实数m的值.
点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,属于基础题.
 |2=(2
|2=(2 +
+ )2 =4
)2 =4 2 +4
2 +4 •
• +
+ 2 =4+4×1×2×cos60°+4=12,
2 =4+4×1×2×cos60°+4=12,故
 .
.(2)因为
 ∥
∥ ,
,所以存在实数λ,使
 =λ
=λ ,即 m
,即 m -
- =λ(2
=λ(2 +
+ ).
).又
 ,
, 不共线,
不共线,所以2λ=m,λ=-1,
解得m=-2.
分析:(1)根据)|
 |2=(2
|2=(2 +
+ )2 =4
)2 =4 2 +4
2 +4 •
• +
+ 2 ,以及|
2 ,以及| |=1,|
|=1,| |=2,求出|
|=2,求出| |2的值,即可得到
|2的值,即可得到 的模.
的模.(2)有题意知 存在实数λ,使
 =λ
=λ ,即 m
,即 m -
- =λ(2
=λ(2 +
+ ),可得 2λ=m,λ=-1,由此求得实数m的值.
),可得 2λ=m,λ=-1,由此求得实数m的值.点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,属于基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 、
、 满足
满足 ,则
,则 .
. ,实数
,实数 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) B.1 C.
B.1 C. D.
D.
 ,
, 满足
满足 ,
, ,
, ,则
,则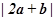 的值为_______.
的值为_______.