题目内容
(本题满分12分)
在△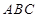 中,角
中,角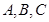 所对的边分别为
所对的边分别为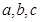 ,已知
,已知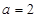 ,
,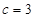 ,
,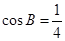 .
.
(1)求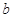 的值;
的值;
(2)求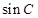 的值.
的值.
在△
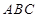 中,角
中,角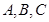 所对的边分别为
所对的边分别为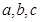 ,已知
,已知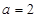 ,
,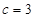 ,
,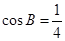 .
.(1)求
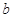 的值;
的值;(2)求
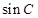 的值.
的值.(1) (2)
(2)
 (2)
(2)
试题分析:解:(1)由余弦定理,
 ,
,得
 ,
,
 .
.(2)方法1:由余弦定理,得

 ,
,∵
 是
是 的内角,∴
的内角,∴ .
. 方法2:∵
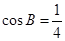 ,且
,且 是
是 的内角,
的内角,∴
 .
.根据正弦定理,
 ,得
,得 .
.点评:熟练的运用正弦定理和余弦定理是解决该试题的关键,同时要根据同角关系式来求解函数值,属于基础题。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 ABC中,A,B,C的对边分别为
ABC中,A,B,C的对边分别为 ,且
,且 则
则 :
: :
: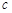 为( )
为( ) :2
:2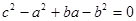 , 则角C的大小为( )
, 则角C的大小为( )



 ,则
,则




 ,则△ABC的最大内角的度数是
,则△ABC的最大内角的度数是  ,则A的度数等于
,则A的度数等于  ,则角C的度数是( )
,则角C的度数是( )