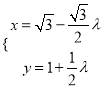题目内容
【题目】设![]() ,函数
,函数![]() .
.
(Ⅰ)若![]() ,求曲线
,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() 无零点,求实数
无零点,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() 有两个相异零点
有两个相异零点![]() ,求证:
,求证: ![]() .
.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() ;(Ⅲ)证明见解析.
;(Ⅲ)证明见解析.
【解析】试题分析:
(Ⅰ)首先求得函数的导数,然后利用导函数研究函数的切线可得曲线![]() 在
在![]() 处的切线方程是
处的切线方程是![]() ;
;
(Ⅱ)结合函数的解析式分类讨论可得实数![]() 的取值范围是
的取值范围是![]() ;
;
(Ⅲ)由题意结合题中的结论构造函数![]() 即可证得题中的不等式.
即可证得题中的不等式.
试题解析:
(Ⅰ)函数的定义域为![]() ,
,
当![]() 时,
时, ![]() ,则切线方程为
,则切线方程为![]() ,即
,即![]() .
.
(Ⅱ)①若![]() 时,则
时,则![]() 是区间
是区间![]() 上的增函数,
上的增函数,
∵![]() ,
,
∴![]() ,函数
,函数![]() 在区间
在区间![]() 有唯一零点;
有唯一零点;
②若![]() 有唯一零点
有唯一零点![]() ;
;
③若![]() ,令
,令![]() ,得
,得![]() ,
,
在区间![]() 上,
上, ![]() ,函数
,函数![]() 是增函数;
是增函数;
在区间![]() 上,
上, ![]() ,函数
,函数![]() 是减函数;
是减函数;
故在区间![]() 上,
上, ![]() 的最大值为
的最大值为![]() ,
,
由于![]() 无零点,须使
无零点,须使![]() ,解得
,解得![]() ,
,
故所求实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)设![]() 的两个相异零点为
的两个相异零点为![]() ,设
,设![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,要证
,要证![]() ,只需证
,只需证![]() ,
,
只需![]() ,等价于
,等价于![]() ,
,
设![]() 上式转化为
上式转化为![]() ),
),
设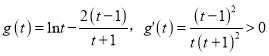 ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
【题目】“累积净化量![]() ”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据
”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据![]() 《空气净化器》国家标准,对空气净化器的累计净化量
《空气净化器》国家标准,对空气净化器的累计净化量![]() 有如下等级划分:
有如下等级划分:
累积净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器(共5000台)的质量,随机抽取![]() 台机器作为样本进行估计,已知这
台机器作为样本进行估计,已知这![]() 台机器的累积净化量都分布在区间
台机器的累积净化量都分布在区间![]() 中,按照
中,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均匀分组,其中累积净化量在
均匀分组,其中累积净化量在![]() 的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
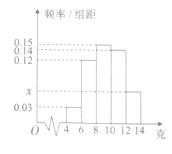
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共5000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累积净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.