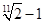题目内容
已知 在区间
在区间 上是增函数,则a的取值范围是( )
上是增函数,则a的取值范围是( )
| A.(0,1) | B. | C. | D. |
C
解析试题分析:∵ 在区间
在区间 上是增函数,∴函数
上是增函数,∴函数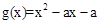 >0在区间
>0在区间 上成立且
上成立且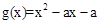 在区间
在区间 上是减函数,∴
上是减函数,∴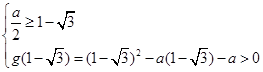 ,∴
,∴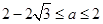 ,故选C
,故选C
考点:本题考查了复合函数的单调性
点评:此类问题除了要运用复合函数的单调性之外,还要注意对数函数的定义域的限制

练习册系列答案
相关题目
函数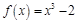 的零点所在的区间是( )
的零点所在的区间是( )
A.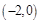 | B.(0,1) | C.(1,2) | D.(2,3) |
已知函数 ,若
,若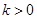 ,则函数
,则函数 的零点个数是
的零点个数是
| A.1 | B.4 | C.3 | D.2 |
设 ,且
,且 ,则
,则
A. | B.10 | C.20 | D.100 |
已知 ,则
,则 的值为( )
的值为( )
A. | B. | C.1 | D.2 |
设函数 在点
在点 处连续,则
处连续,则
A. | B. | C. | D. |
对数式 有意义,则实数
有意义,则实数 的取值范围是
的取值范围是
| A.(3,4)∪(4,7) | B.(3,7) | C.(-∞,7) | D.(3,+∞) |
设 是奇函数,且在
是奇函数,且在 内是增函数,又
内是增函数,又 ,则
,则 的解集是 ( )
的解集是 ( )
A. | B. |
C. | D. |