题目内容
已知抛物线y2=2px(p>0),过点E(m,0)(m≠0)的直线交抛物线与点M,N,交y轴于点P,若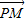 =λ
=λ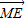 ,
,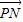 =μ
=μ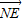 ,则λ+μ=( )
,则λ+μ=( )A.1
B.-1
C.2
D.-2
【答案】分析:设M,N,P的坐标,由已知的向量等式把M,N的坐标用λ,μ和P的坐标表示,设出过点E(m,0)(m≠0)的直线方程,和抛物线方程联立后写出根与系数关系,结合M点的坐标适合直线方程联立整理即可得到答案.
解答:解:分别设M,N,P的坐标为(x1,y1),(x2,y2),(0,y),由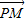 =λ
=λ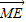 ,
,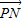 =μ
=μ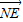 ,
,
∴(x1,y1-y)=λ(m-x1,-y1),(x2,y2-y)=μ(m-x2,-y2),
可得到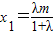 ,
,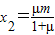 ,
,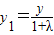 ,
,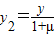 ,
,
直线MN的方程为:x=ty+m,
把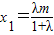 ,
,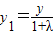 ,代入x=ty+m得:
,代入x=ty+m得: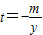 ①
①
把x=ty+m,代入y2=2px,得y2-2pty-2pm=0.
∴y1+y2=2pt,y1y2=-2pm.
∴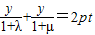 ②
②
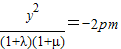 ③
③
联立①②③得λ+μ=-1.
故选B.
点评:本题考查了直线与援锥曲线的综合题,考查了平面向量在解题中的应用,解答此题的关键在于大胆的设出点的坐标及直线方程,灵活运用已知条件列式消去未知量,体现了整体运算思想,是难题.
解答:解:分别设M,N,P的坐标为(x1,y1),(x2,y2),(0,y),由
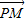 =λ
=λ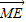 ,
,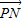 =μ
=μ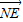 ,
,∴(x1,y1-y)=λ(m-x1,-y1),(x2,y2-y)=μ(m-x2,-y2),
可得到
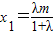 ,
,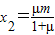 ,
,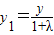 ,
,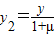 ,
,直线MN的方程为:x=ty+m,
把
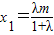 ,
,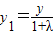 ,代入x=ty+m得:
,代入x=ty+m得: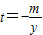 ①
①把x=ty+m,代入y2=2px,得y2-2pty-2pm=0.
∴y1+y2=2pt,y1y2=-2pm.
∴
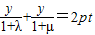 ②
②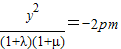 ③
③联立①②③得λ+μ=-1.
故选B.
点评:本题考查了直线与援锥曲线的综合题,考查了平面向量在解题中的应用,解答此题的关键在于大胆的设出点的坐标及直线方程,灵活运用已知条件列式消去未知量,体现了整体运算思想,是难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目