题目内容
已知数列{an}的前n项和为Sn,函数f(x)= px3-
px3- (p+q)x2+qx+q(其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值、点(n,2Sn)(n∈N+)均在函数y=2px2-qx+q-f′(x)的图象上.
(p+q)x2+qx+q(其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值、点(n,2Sn)(n∈N+)均在函数y=2px2-qx+q-f′(x)的图象上.
(1)求a1的值;
(2)求数列{an}的通项公式.
解:(1)函数f(x)的定义域为(-∞,+∞),f'(x)=px2-(p+q)x+q,
令f'(x)=0,得x=1或x= .又因为p>q>0,故有0<
.又因为p>q>0,故有0<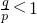 .
.
再由f'(x)在x=1的左侧为负、右侧为正,故当x=1时,函数f(x)取得极小值.
再由f'(x)在x= 的左侧为正、右侧为负,故当x=
的左侧为正、右侧为负,故当x= 时,函数f(x)取得极大值.
时,函数f(x)取得极大值.
由于当x=a1时,函数f(x)取得极小值,故 a1 =1.
(2)函数y=2px2-qx+q-f′(x)=px2+px,
点(n,2Sn)(n∈N+)均在函数y=2px2-qx+q-f′(x)的图象上,
故有 2Sn =pn2+pn ①,故 2sn-1=p(n-1)2+p(n-1),(n>1 ) ②.
把①②相减可得 2an=2pn,∴an=pn.
再由a1 =1可得 p=1,故an=n.
综上可得,数列{an}的通项公式为 an=n.
分析:(1)先对函数f(x)进行求导,令其导数为0求得x,进而根据x变化时f'(x)和f(x)的变化情况确定函数f(x)的极小值.求得a1.
(2)点(n,2Sn)(n∈N+)均在函数y=2px2-qx+q-f′(x)的图象上,可得 2Sn =pn2+pn ①,换元可得 2sn-1=p(n-1)2+p(n-1)②,把①②相减可得 2an=2pn,再由 a1 =1求得数列{an}的通项公式.
点评:本题主要考查了数列与函数的综合,涉及了函数的导数求极值,数列递推式求通项公式等.考查了考试综合分析问题和解决问题的能力,属于中档题.
令f'(x)=0,得x=1或x=
 .又因为p>q>0,故有0<
.又因为p>q>0,故有0<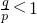 .
.再由f'(x)在x=1的左侧为负、右侧为正,故当x=1时,函数f(x)取得极小值.
再由f'(x)在x=
 的左侧为正、右侧为负,故当x=
的左侧为正、右侧为负,故当x= 时,函数f(x)取得极大值.
时,函数f(x)取得极大值.由于当x=a1时,函数f(x)取得极小值,故 a1 =1.
(2)函数y=2px2-qx+q-f′(x)=px2+px,
点(n,2Sn)(n∈N+)均在函数y=2px2-qx+q-f′(x)的图象上,
故有 2Sn =pn2+pn ①,故 2sn-1=p(n-1)2+p(n-1),(n>1 ) ②.
把①②相减可得 2an=2pn,∴an=pn.
再由a1 =1可得 p=1,故an=n.
综上可得,数列{an}的通项公式为 an=n.
分析:(1)先对函数f(x)进行求导,令其导数为0求得x,进而根据x变化时f'(x)和f(x)的变化情况确定函数f(x)的极小值.求得a1.
(2)点(n,2Sn)(n∈N+)均在函数y=2px2-qx+q-f′(x)的图象上,可得 2Sn =pn2+pn ①,换元可得 2sn-1=p(n-1)2+p(n-1)②,把①②相减可得 2an=2pn,再由 a1 =1求得数列{an}的通项公式.
点评:本题主要考查了数列与函数的综合,涉及了函数的导数求极值,数列递推式求通项公式等.考查了考试综合分析问题和解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |