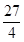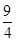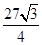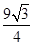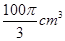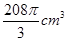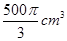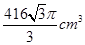题目内容
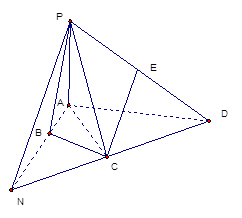
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2。
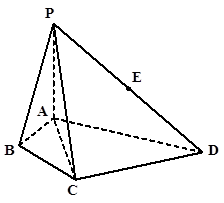
(1)求证:CE∥平面PAB;
(2)求四面体PACE的体积.
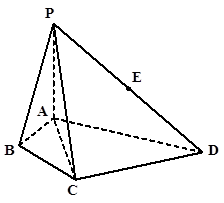
(1)求证:CE∥平面PAB;
(2)求四面体PACE的体积.
(1)详见解析;(2)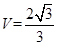
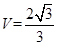
试题分析:(1)要证CE∥平面PAB,可以转换为证明
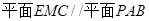 ,而要证明
,而要证明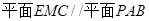 又可转化为
又可转化为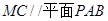 与
与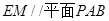 (另外也可以转化为线线平行) ;(2)要求四面体PACE的体积,可转换顶点求以E为顶点PAC为底面的三棱锥的体积.
(另外也可以转化为线线平行) ;(2)要求四面体PACE的体积,可转换顶点求以E为顶点PAC为底面的三棱锥的体积.试题解析:(1)法一:取AD得中点M,连接EM,CM.
则EM//PA 1分
因为
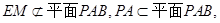
所以,
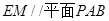 2分
2分在
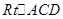 中,
中,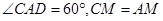
所以,
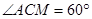
而
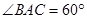 ,所以,MC//AB. 3分
,所以,MC//AB. 3分因为
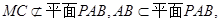
所以,
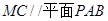 4分
4分又因为
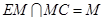
所以,
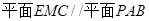
因为
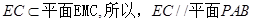 6分
6分法二: 延长DC,AB,交于N点,连接PN. 1分
因为
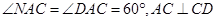
所以,C为ND的中点. 3分
因为E为PD的中点,所以,EC//PN
因为
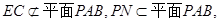
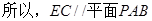 6分
6分(2)法一:由已知条件有;AC=2AB=2,AD=2AC=4,CD=
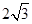 7分
7分 因为,
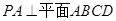 ,所以,
,所以,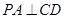 8分
8分又因为
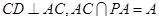
所以,
 10分
10分因为E是PD的中点
所以点E平面PAC的距离
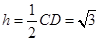 ,
,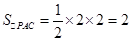
所以,四面体PACE的体积
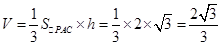 12分
12分法二:由已知条件有;AC=2AB=2,AD=2AC=4,CD=
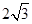
因为,
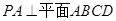
所以,
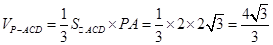 10分
10分因为E是PD的中点
所以,四面体PACE的体积
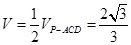 12分
12分
练习册系列答案
相关题目
 是边长为6的等边三角形,
是边长为6的等边三角形, 分别为
分别为 靠近
靠近 的三等分点,点
的三等分点,点 为边
为边 边的中点,线段
边的中点,线段 交线段
交线段 于点
于点 .将
.将 沿
沿 平面
平面 ,连接
,连接 ,形成如图乙所示的几何体.
,形成如图乙所示的几何体.
 平面
平面
 的体积.
的体积. 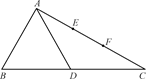
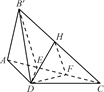
 中,
中,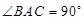 ,
,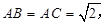
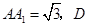 是
是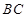 中点,
中点,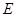 是
是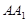 中点.
中点.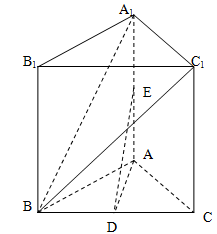
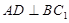 ;
;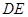 ∥面
∥面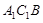 .
. 内接于球
内接于球 ,且底面边长为
,且底面边长为 ,侧棱长为2,则球
,侧棱长为2,则球

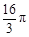

 中,
中,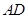 与
与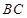 互相垂直,
互相垂直,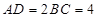 ,且
,且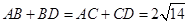 ,则四面体
,则四面体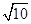
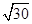
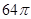


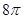
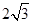 ,底面是等边三角形,则这个三棱锥的体积为( )
,底面是等边三角形,则这个三棱锥的体积为( )