题目内容

已知圆O：x²+y²=4，圆O与x轴交于A，B两点，过点B的圆的切线为l，P是圆上异于A，B的一点，PH垂直于x轴，垂足为H，E是PH的中点，延长AP，AE分别交l于F，C．
（1）若点P（1， $数学公式$ ），求以FB为直径的圆的方程，并判断P是否在圆上；
（2）当P在圆上运动时，证明：直线PC恒与圆O相切．

（1）证明：由P（1， $\text{[math]}$ ），A（-2，0）
∴直线AP的方程为 $\text{[math]}$ ．
令x=2，得F（2， $\text{[math]}$ ）．（2分）
由E（1， $\text{[math]}$ ），A（-2，0），则直线AE的方程为y= $\text{[math]}$ （x+2），
令x=2，得C（2， $\text{[math]}$ ）．（4分）
∴C为线段FB的中点，以FB为直径的圆恰以C为圆心，半径等于 $\text{[math]}$ ．
∴圆的方程为 $\text{[math]}$ ，且P在圆上；
（2）证明：设P（x₀，y₀），则E（x₀， $\text{[math]}$ ），则直线AE的方程为 $\text{[math]}$
在此方程中令x=2，得C（2， $\text{[math]}$ ）
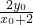直线PC的斜率为 $\text{[math]}$ =- $\text{[math]}$ =- $\text{[math]}$
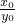
若x₀=0，则此时PC与y轴垂直，即PC⊥OP；（13分）
若x₀≠0，则此时直线OP的斜率为 $\text{[math]}$ ，
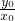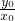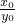∵ $\text{[math]}$ ×（- $\text{[math]}$ ）=-1
∴PC⊥OP
∴直线PC与圆O相切．（16分）
分析：（1）先确定直线AP的方程为 $\text{[math]}$ ，求得F（2， $\text{[math]}$ ），确定直线AE的方程为y= $\text{[math]}$ （x+2），求得C（2， $\text{[math]}$ ），由此可得圆的方程；
（2）设P（x₀，y₀），则E（x₀， $\text{[math]}$ ），求得直线AE的方程，进而可确定直线PC的斜率，由此即可证得直线PC与圆O相切．
点评：本题考查直线与圆的位置关系，考查圆的方程，解题的关键是确定圆的圆心与半径，利用斜率关系确定直线与圆相切．