题目内容
已知数列{an}满足a1=3,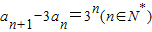 ,数列{bn}满足
,数列{bn}满足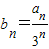 .
.(1)证明数列{bn}是等差数列并求数列{bn}的通项公式;
(2)求数列{an}的前n项和Sn.
【答案】分析:(1)由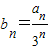 ,可得
,可得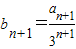 ,然后检验bn+1-bn是否为常数即可证明,进而可求其通项
,然后检验bn+1-bn是否为常数即可证明,进而可求其通项
(2)由题意可先求an,结合数列的通项的特点,考虑利用错位相减求和即可求解
解答:解(1)证明:由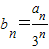 ,得
,得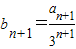 ,
,
∴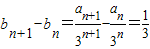 ---------------------(2分)
---------------------(2分)
所以数列{bn}是等差数列,首项b1=1,公差为 -----------(4分)
-----------(4分)
∴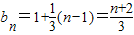 ------------------------(6分)
------------------------(6分)
(2)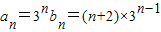 -------------------------(7分)
-------------------------(7分)
∴Sn=a1+a2+…+an=3×1+4×3+…+(n+2)×3n-1----①
∴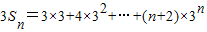 -------------------②(9分)
-------------------②(9分)
①-②得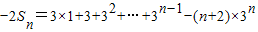
=2+1+3+32+…+3n-1-(n+2)×3n=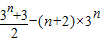 ------(11分)
------(11分)
∴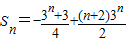 -----------------(12分)
-----------------(12分)
点评:本题主要考查了利用数列的递推公式证明等差数列,及等差数列的通项公式的应用,数列的错位相减求和方法的应用.
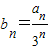 ,可得
,可得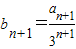 ,然后检验bn+1-bn是否为常数即可证明,进而可求其通项
,然后检验bn+1-bn是否为常数即可证明,进而可求其通项(2)由题意可先求an,结合数列的通项的特点,考虑利用错位相减求和即可求解
解答:解(1)证明:由
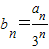 ,得
,得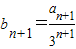 ,
,∴
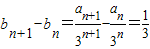 ---------------------(2分)
---------------------(2分)所以数列{bn}是等差数列,首项b1=1,公差为
 -----------(4分)
-----------(4分)∴
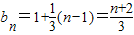 ------------------------(6分)
------------------------(6分)(2)
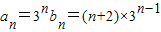 -------------------------(7分)
-------------------------(7分)∴Sn=a1+a2+…+an=3×1+4×3+…+(n+2)×3n-1----①
∴
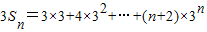 -------------------②(9分)
-------------------②(9分)①-②得
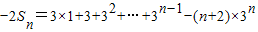
=2+1+3+32+…+3n-1-(n+2)×3n=
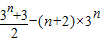 ------(11分)
------(11分)∴
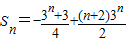 -----------------(12分)
-----------------(12分)点评:本题主要考查了利用数列的递推公式证明等差数列,及等差数列的通项公式的应用,数列的错位相减求和方法的应用.

练习册系列答案
相关题目