题目内容
17.如果实数x,y满足$\left\{\begin{array}{l}{x-2y+5≥0}\\{3-x≥0}\\{x+2y+5≥0}\end{array}\right.$,表示的平面区域D,且圆C的方程为x2+y2=25,(1)在圆C内部或边界上任取一点,求该点落在区域D内的概率.
(2)在圆C内部或边界上任取一整点(纵横坐标都是整数的点),求该整点落在区域D内的概率.
分析 (1)作出不等式组对应的平面区域,求出对应的面积,利用几何概型的概率公式即可求该点落在区域D内的概率.
(2)利用列举法求出对应的整点格式,利用古典概型的概率公式进行求解即可.
解答 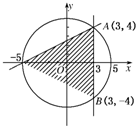 解:(Ⅰ)由题意知,区域D在圆内,如图所示.设“在圆C内部或边界上任取一点,求点落在区域D内”为事件A,由于圆C的面积为25π,而区域D的面积为$\frac{1}{2}×8×8=32$,
解:(Ⅰ)由题意知,区域D在圆内,如图所示.设“在圆C内部或边界上任取一点,求点落在区域D内”为事件A,由于圆C的面积为25π,而区域D的面积为$\frac{1}{2}×8×8=32$,
由几何概型概率计算公式可得,在圆C内部或边界上任取一点,落在区域D内的概率P(A)=$\frac{32}{25π}$,
(Ⅱ)设“在圆C内部或边界上任取一整点,整点落在区域D内”为事件
B,由圆C的对称性,第一象限内及x轴正半轴上的整点有
(4,1),(4,2),(4,3),(3,1),(3,2),(3,3),(3,4),(2,1),(2,2),(2,3),(2,4),
(1,1),(1,2),(1,3),(1,4),(5,0),(4,0),(3,0),(2,0),(1,0),
共计20个,所以圆C内部或边界上整点共计20×4+1=81个,其中落在区域D内的整点在x轴上方的有
(-3,1),(-2,1),(-1,1),(-1,2),(0,1),(0,2),(1,1),(1,2),(1,3),(2,1),(2,2),
(2,3),(3,1),(3,2),(3,3),(3,4),共计16个,
根据区域D关于x轴对称,故落在区域D内的整点有16×2+9=41个,
所以圆C内部或边界上任取一整点,整点落在区域D内的概率P(B)=$\frac{41}{81}$.
点评 本题主要考查概率的计算,要求熟练掌握几何概型和古典概型的概率的计算.

练习册系列答案
相关题目
7.一个几何体的三视图如图,则该几何体的体积为( )


| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
5.执行如图所示的程序框图,要使输出的S的值小于1,则输入的t值不能是下面的( )


| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
 已知,如图,抛物线C:y2=2px(p>0)经过点P(2,4),直线l:y=$\sqrt{3}x-2\sqrt{3}$交C于A、B两点,与x轴相交于点F.
已知,如图,抛物线C:y2=2px(p>0)经过点P(2,4),直线l:y=$\sqrt{3}x-2\sqrt{3}$交C于A、B两点,与x轴相交于点F.