题目内容
2. 在梯形ABCD中,AB=a,CD=b,a<b,EF为一线段,若S四边形ABFE=S四边形CDEF,且∠BFE=∠D,求EF的长(用a,b表示).
在梯形ABCD中,AB=a,CD=b,a<b,EF为一线段,若S四边形ABFE=S四边形CDEF,且∠BFE=∠D,求EF的长(用a,b表示).
分析 根据相似三角形的性质得到比例式,求出EF的长即可.
解答 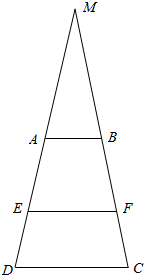 解:如图示:延长DA、CB交于点M,设△MAB面积=s,
解:如图示:延长DA、CB交于点M,设△MAB面积=s,
∵AB∥CD
∴∠MAB=∠ADC,又由∠M是公共角,
∴△MAB∽△MDC
∴$\frac{{S}_{△MAB}}{{S}_{△MDC}}$=$\frac{{AB}^{2}}{{CD}^{2}}$,即:$\frac{s}{{S}_{△MDC}}$=$\frac{{a}^{2}}{{b}^{2}}$,∴S△MDC=$\frac{{sb}^{2}}{{a}^{2}}$,
∴S梯形ABCD=S△MDC-S△MAB=$\frac{s{(b}^{2}{-a}^{2})}{{a}^{2}}$,
∵四边形ABFE的面积与四边形CDEF的面积相等,
∴S四边形ABEF=$\frac{1}{2}$S梯形ABCD=$\frac{1}{2}$•$\frac{s{(b}^{2}{-a}^{2})}{{a}^{2}}$,
∴S△MEF=S△MAB+S四边形ABEF=s+$\frac{s{(b}^{2}{-a}^{2})}{{2a}^{2}}$=$\frac{s{(b}^{2}{+a}^{2})}{{2a}^{2}}$,
∵∠BFE=∠ADC
∴∠MAB=∠BFE,又∠M是公共角,
∴△MAB∽△MFE
∴$\frac{{S}_{△MAB}}{{S}_{△MEF}}$=$\frac{{AB}^{2}}{{EF}^{2}}$,即:$\frac{s}{\frac{s{(b}^{2}{+a}^{2})}{{2a}^{2}}}$=$\frac{{a}^{2}}{{EF}^{2}}$,
∴EF2=$\frac{{a}^{2}{+b}^{2}}{2}$,
∵EF>0
∴EF=$\frac{\sqrt{{a}^{2}{+b}^{2}}}{2}$.
点评 本题考查了相似三角形的性质的应用,是一道中档题.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | 56 | B. | 55 | C. | 54 | D. | 53 |