题目内容
品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出n瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这n瓶酒,并重新按品质优劣为它们排序,这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评为.现设n=4,分别以a1,a2,a3,a4表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令X=|1-a1|+|2-a2|+|3-a3|+|4-a4|,
则X是对两次排序的偏离程度的一种描述.
(Ⅰ)写出X的可能值集合;
(Ⅱ)假设a1,a2,a3,a4等可能地为1,2,3,4的各种排列,求X的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中,都有X≤2,
①试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);②你认为该品酒师的酒味鉴别功能如何?说明理由.
分析:(1)X的可能取值集合为{0、2、4、6、8},在1、2、3、4中奇数与偶数各有两个,a2,a4中的奇数个数等于a1,a3中的偶数个数,得到|1-a1|+|3-a3|与|2-a2|+|4-a4|的奇偶性相同,得到结论.
(2)可以用列表或者树状图列出1、2、3、4的一共24种排列,计算每种排列下的X的值,算出概率,写出分布列.
(3)做出三轮测试都有X≤2的概率,记做P,做出概率的值和已知量进行比较,得到结论,
(2)可以用列表或者树状图列出1、2、3、4的一共24种排列,计算每种排列下的X的值,算出概率,写出分布列.
(3)做出三轮测试都有X≤2的概率,记做P,做出概率的值和已知量进行比较,得到结论,
解答:解:(1)X的可能取值集合为{0、2、4、6、8}
∵在1、2、3、4中奇数与偶数各有两个,
∴a2,a4中的奇数个数等于a1,a3中的偶数个数,
∴|1-a1|+|3-a3|与|2-a2|+|4-a4|的奇偶性相同,
∴X=(|1-a1|+|3-a3|)+(|2-a2|+|4-a4|)必为偶数,
X的值非负,且易知其值不大于8,
∴X的可能取值集合为{0、2、4、6、8}
(2)可以用列表或者树状图列出1、2、3、4的一共24种排列,
计算每种排列下的X的值,
在等可能的假定下,
得到P(X=0)=
P(X=2)=
P(X=4)=
P(X=6)=
P(X=8)=
(3)①首先P(X≤2)=P(X=0)+P(X=2)=
=
将三轮测试都有X≤2的概率记做P,有上述结果和独立性假设得
P=(
)3=
,
②由于P=
<
是一个很小的概率,
这表明仅凭随机猜测得到三轮测试都有X≤2的结果的可能性很小,
∴我们认为该品酒师确实有良好的鉴别功能,不是靠随机猜测.
∵在1、2、3、4中奇数与偶数各有两个,
∴a2,a4中的奇数个数等于a1,a3中的偶数个数,
∴|1-a1|+|3-a3|与|2-a2|+|4-a4|的奇偶性相同,
∴X=(|1-a1|+|3-a3|)+(|2-a2|+|4-a4|)必为偶数,
X的值非负,且易知其值不大于8,
∴X的可能取值集合为{0、2、4、6、8}
(2)可以用列表或者树状图列出1、2、3、4的一共24种排列,
计算每种排列下的X的值,
在等可能的假定下,
得到P(X=0)=
| 1 |
| 24 |
P(X=2)=
| 3 |
| 24 |
P(X=4)=
| 7 |
| 24 |
P(X=6)=
| 9 |
| 24 |
P(X=8)=
| 4 |
| 24 |
(3)①首先P(X≤2)=P(X=0)+P(X=2)=
| 4 |
| 24 |
| 1 |
| 6 |
将三轮测试都有X≤2的概率记做P,有上述结果和独立性假设得
P=(
| 1 |
| 6 |
| 1 |
| 216 |
②由于P=
| 1 |
| 216 |
| 5 |
| 1000 |
这表明仅凭随机猜测得到三轮测试都有X≤2的结果的可能性很小,
∴我们认为该品酒师确实有良好的鉴别功能,不是靠随机猜测.
点评:本题主要考查分布列和期望的简单应用,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,只要注意解题格式就问题不大.

练习册系列答案
相关题目
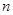 瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这
瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这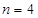 ,分别以
,分别以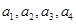 表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令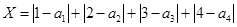 ,
,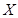 是对两次排序的偏离程度的一种描述。
是对两次排序的偏离程度的一种描述。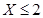 ,
,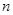 瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这
瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这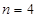 ,分别以
,分别以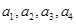 表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令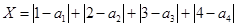 ,
,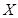 是对两次排序的偏离程度的一种描述。
是对两次排序的偏离程度的一种描述。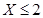 ,
,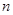 瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这
瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这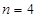 ,分别以
,分别以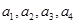 表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令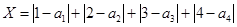 ,
,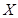 是对两次排序的偏离程度的一种描述。
是对两次排序的偏离程度的一种描述。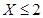 ,
,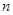 瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这
瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这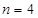 ,分别以
,分别以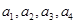 表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令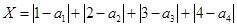 ,
,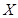 是对两次排序的偏离程度的一种描述。
是对两次排序的偏离程度的一种描述。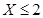 ,
,