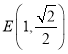题目内容
【题目】已知长为3的线段
的两端点
，
分别在
轴和
轴上移动，
.
（1）求点
的轨迹
的方程.
（2）过
作互相垂直的两条直线分别与轨迹交于，和
，
，设中点为
，
中点为
，试探究直线
是否过定点？若是，求出该定点；若不是，说明理由.
【答案】（1）
（2）直线
过定点
【解析】
（1）设
，由
得
，
，然后利用
，即可求解.
（2）若直线
斜率存在且不为0.设直线的方程为
，代入椭圆方程，求得
的坐标，同理设
的方程为
，代入椭圆方程，求得
的坐标，然后可得直线的直线方程，化简后即可求出过定点.
解：（1）设，由得，，
，整理得点
的轨迹
的方程为.
（2）若直线斜率存在且不为0.设直线的方程为，
与椭圆方程联立得
，
显然
，设
，
坐标分别为
，
，中点坐标为
，
则
，
，
即
.
同理可得，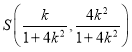
，
.
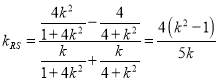直线的方程为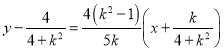
，
整理得
.
当直线斜率不存在或为0时，直线即为
轴，也过点.
综上，直线过定点.
练习册系列答案
名校课堂系列答案
相关题目
【题目】为了调查某款电视机的寿命，研究人员对该款电视机进行了相应的测试，将得到的数据分组：
，
，
，
，
，并统计如图所示：
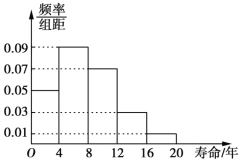
并对不同性别的市民对这款电视机的购买意愿作出调查，得到的数据如下表所示：
愿意购买该款电视机 | 不愿意购买该款电视机 | 总计 | |
男性 | 800 | 1000 | |
女性 | 600 | ||
总计 | 1200 |
（1）根据图中的数据，试估计该款电视机的平均寿命；
（2）根据表中数据，能否在犯错误的概率不超过0.001的前提下认为“是否愿意购买该款电视机”与“市民的性别”有关；
（3）以频率估计概率，若在该款电视机的生产线上随机抽取4台，记其中寿命不低于4年的电视机的台数为X，求X的分布列及数学期望.
参考公式及数据：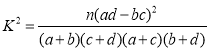
，其中
．
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
