题目内容
在某批次的某种灯泡中,随机地抽取 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
| 寿命(天) | 频数 | 频率 |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
| 合计 |  |  |
 、
、 的值;
的值;(2)某人从灯泡样品中随机地购买了
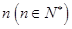 个,如果这
个,如果这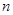 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求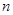 的最小值;
的最小值;(3)某人从这个批次的灯泡中随机地购买了
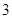 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求 的分布列和数学期望.
的分布列和数学期望.
(1) ,
, ;(2)
;(2) ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)根据频数之和为 以及频率之和为
以及频率之和为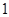 分别求出
分别求出 、
、 的值;(2)先确定灯泡中优等品、正品、次品的个数,计算三者之间的比例,从而确定灯泡数的表达式,进而确定
的值;(2)先确定灯泡中优等品、正品、次品的个数,计算三者之间的比例,从而确定灯泡数的表达式,进而确定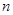 的最小值;(3)先确定随机变量
的最小值;(3)先确定随机变量 的可能取值,根据题中条件确定
的可能取值,根据题中条件确定 在不同取值下的概率,并列出相应的分布列,求出数学期望.
在不同取值下的概率,并列出相应的分布列,求出数学期望.
试题解析:(1) ,
, .
.
(2)由表可知:灯泡样品中优等品有 个,正品有
个,正品有 个,次品有
个,次品有 个,
个,
所以优等品、正品和次品的比例为 .
.
所以按分层抽样法,购买灯泡数 ,
,
所以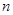 的最小值为
的最小值为 ;
;
(3) 的所有取值为
的所有取值为 .
.
由题意,购买一个灯泡,且这个灯泡是次品的概率为 ,
,
从本批次灯泡中购买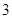 个,可看成
个,可看成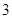 次独立重复试验,
次独立重复试验,
所以 ,
, ,
, ,
, .
.
所以随机变量 的分布列为:
的分布列为:
所以

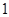
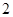
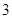
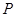




 的数学期望
的数学期望 .
.
(注:写出 ,
, ,
, 、
、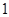 、
、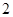 、
、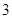 .请酌情给分)
.请酌情给分)
考点:1.频率分布表;2.分层抽样;3.二项分布

练习册系列答案
相关题目
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.
附:
| P(K2≥x0) | 0.050 | 0.010 | 0.001 |
| x0 | 3.841 | 6.635 | 10.828 |
χ2=

为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
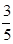 .
.(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中,
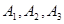 还喜欢打羽毛球,
还喜欢打羽毛球,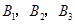 还喜欢打乒乓球,
还喜欢打乒乓球,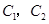 还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求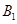 和
和 不全被选中的概率.
不全被选中的概率.下面的临界值表供参考:
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
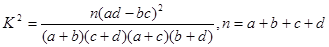 )
) 某单位有2000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如下表所示:
| 人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
| 老年 | 40 | 40 | 40 | 80 | 200 |
| 中年 | 80 | 120 | 160 | 240 | 600 |
| 青年 | 40 | 160 | 280 | 720 | 1 200 |
| 小计 | 160 | 320 | 480 | 1 040 | 2 000 |
(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?
一家商场为了确定营销策略,进行了投入促销费用x和商场实际销售额y的试验,得到如下四组数据.
| 投入促销费用x(万元) | 2 | 3 | 5 | 6 |
| 商场实际营销额y(万元) | 100 | 200 | 300 | 400 |
(2)求出x,y之间的回归直线方程
 =
= x+
x+ ;
;(3)若该商场计划营销额不低于600万元,则至少要投入多少万元的促销费用?
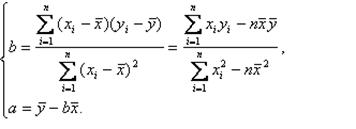
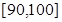 内的记为
内的记为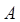 ,其中“语文”科目成绩在
,其中“语文”科目成绩在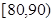 内的考生有10人.
内的考生有10人.
 名学生的成绩得到频率分布直方图如下:
名学生的成绩得到频率分布直方图如下:
 和
和 的学生中共抽取
的学生中共抽取 人,该
人,该 人,求分数在
人,求分数在 人的概率.
人的概率.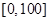 ,样本数据分组为
,样本数据分组为 ,
,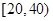 ,
,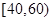 ,
,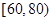 ,
,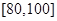 .
.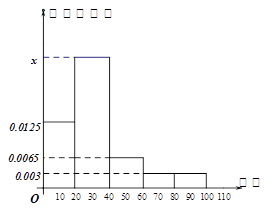
 的值;
的值;