Question

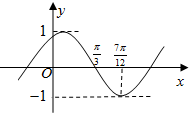已知函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜

π

2

）的部分图象如图所示，则f(

π

4

)的值为（　　）

• A、

  1

  2

• B、

  3

  5

• C、

  4

  5

• D、1

Answer 1

分析：由图象可得A和周期T，进而可得ω，又图象过点（

π

3

，0），可得φ的方程，结合范围可得φ值，可得解析式，代值化简可得．

解答：解：由图象可得A=1，周期T=4（

7π

12

-

π

3

）=π，
∴ω=

2π

T

=2，
∴f（x）=sin（2x+φ），
又图象过点（

π

3

，0），
∴0=sin（

2π

3

+φ），
又∵|φ|＜

π

2

，
∴φ=

π

3

∴f（x）=sin（2x+

π

3

），
∴f(

π

4

)=sin（

π

2

+

π

3

）=

1

2

故选：A

点评：本题考查由三角函数的图象求解析式，属基础题．