题目内容
已知曲线![]() 的一条切线的斜率为
的一条切线的斜率为![]() ,,则切点的横坐标为 .
,,则切点的横坐标为 .
考点:
利用导数研究曲线上某点切线方程.
专题:
计算题.
分析:
求出曲线方程的导函数,根据切线的方程找出切线的斜率,令导函数等于斜率列出关于x的方程,求出方程的解即为切点的横坐标.
解答:
解:求导函数得:y′=![]() ﹣
﹣![]() (x>0),又由曲线的一条切线的斜率为
(x>0),又由曲线的一条切线的斜率为![]() ,
,
令![]() ﹣
﹣![]() =
=![]() 即(x﹣3)(x+2)=0,解得x=3,x=﹣2(不合题意,舍去),
即(x﹣3)(x+2)=0,解得x=3,x=﹣2(不合题意,舍去),
则切点的横坐标为3.
故答案为:3
点评:
此题考查学生会利用导数求曲线上过某点切线方程的斜率,是一道基础题.学生在求出x的值后,注意隐含的条件函数的定义域x>0,舍去不合题意的x的值.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标为( )
,则切点的横坐标为( )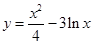 的一条切线的斜率为
的一条切线的斜率为 ,则该切线的切点横坐标为
,则该切线的切点横坐标为
 B.
B.
 C.
C.
 D.
D.
 的一条切线的斜率为2,则该切线的方程为
。
的一条切线的斜率为2,则该切线的方程为
。 的一条切线的斜率为
的一条切线的斜率为 ,则切点的纵坐标为 ▲
,则切点的纵坐标为 ▲