题目内容
求下面各数列的一个通项:(1)-
| 1 |
| 2×4 |
| 4 |
| 5×7 |
| 9 |
| 8×10 |
| 16 |
| 11×13 |
(2)数列的前n项的和Sn=2n2+n+1;
(3)数列{an}的前n项和Sn=1+ran(r为不等于0,1的常数).
分析:(1)先根据各项的符号确定(-1)n,再由各项分子是序号的平方从而可得到分子为n2,再由分母的形式可确定分母为(3n-1)(3n+1),进而可确定数列的通项公式.
(2)先令n=1可得到a1的值,再由当n≥2时,an=Sn-Sn-1=4n-1,最后验证当n=1时的值,得到答案.
(3)先根据Sn=1+ran可得到Sn-1=1+ran-1,再由当n≥2时an=Sn-Sn-1=r(an-an-1),可得到
=
,可确定数列{an}是公比为
的等比数列,最后根据等比数列的通项公式可得到答案.
(2)先令n=1可得到a1的值,再由当n≥2时,an=Sn-Sn-1=4n-1,最后验证当n=1时的值,得到答案.
(3)先根据Sn=1+ran可得到Sn-1=1+ran-1,再由当n≥2时an=Sn-Sn-1=r(an-an-1),可得到
| an |
| an-1 |
| r |
| r-1 |
| r |
| r-1 |
解答:解:(1)an=(-1)n
.
(2)当n=1时a1=S1=4,当n≥2时an=Sn-Sn-1=4n-1,
显然a1不适合an=4n-1
∴an=
.
(3)由Sn=1+ran可得当n≥2时Sn-1=1+ran-1,
∴Sn-Sn-1=r(an-an-1),
∴an=ran-ran-1,∴an(r-1)=ran-1,∵r≠1,
∴
=
,∵r≠0,
∴{an}是公比为
的等比数列.
又当n=1时,S1=1+ra1,∴a1=
,
∴an=
(
)n-1.
| n2 |
| (3n-1)(3n+1) |
(2)当n=1时a1=S1=4,当n≥2时an=Sn-Sn-1=4n-1,
显然a1不适合an=4n-1
∴an=
|
(3)由Sn=1+ran可得当n≥2时Sn-1=1+ran-1,
∴Sn-Sn-1=r(an-an-1),
∴an=ran-ran-1,∴an(r-1)=ran-1,∵r≠1,
∴
| an |
| an-1 |
| r |
| r-1 |
∴{an}是公比为
| r |
| r-1 |
又当n=1时,S1=1+ra1,∴a1=
| 1 |
| 1-r |
∴an=
| 1 |
| 1-r |
| r |
| r-1 |
点评:本题主要考查求数列通项公式的方法--观察法和利用Sn与an的关系进行转化法.求数列的通项公式是数列考查的重点,要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
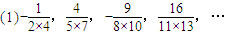 ;
;