题目内容
已知 在
在 与
与 处都取得极值.
处都取得极值.
(1)求 ,
, 的值;
的值;
(2)设函数 ,若对任意的
,若对任意的 ,总存在
,总存在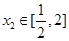 ,使得:
,使得: ,求实数
,求实数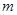 的取值范围.
的取值范围.
(1)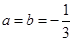 ;(2)
;(2)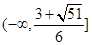 .
.
解析试题分析:(1)根据条件 ,可得
,可得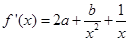 ,由
,由 在
在 与
与 处都取得极值,可知
处都取得极值,可知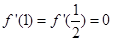 ,故可建立关于
,故可建立关于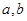 的二元一次方程组,从而解得
的二元一次方程组,从而解得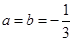 ,此时,需要代回检验
,此时,需要代回检验 是否确实是
是否确实是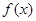 的极值点,经检验
的极值点,经检验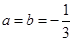 符合题意,从而
符合题意,从而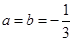 ;(2)由(1)可得由(1)知:函数
;(2)由(1)可得由(1)知:函数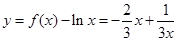 在
在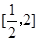 上递减,
上递减,
∴ 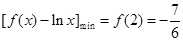 ,因此问题就等价于求使当
,因此问题就等价于求使当 时,
时,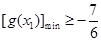 恒成立的
恒成立的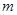 的取值范围,而二次函数
的取值范围,而二次函数 图像的对称轴是
图像的对称轴是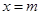 ,因此需对
,因此需对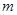 的取值作出以下三种情况的分类讨论:①:
的取值作出以下三种情况的分类讨论:①: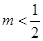 ;②:
;②: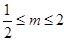 ;③
;③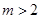 ,分别用含
,分别用含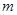 的代数式表示上述三种情况下
的代数式表示上述三种情况下 的最小值表示出来,从而可以建立关于
的最小值表示出来,从而可以建立关于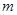 的不等式,进而求得
的不等式,进而求得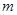 的取值范围为
的取值范围为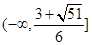 .
.
试题解析:(1)∵ ,∴
,∴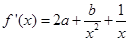 1分
1分
∵ 在
在 与
与 处都取得极值,
处都取得极值,
∴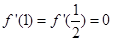 ,∴
,∴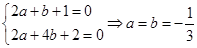 4分
4分
经检验,当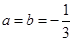 时,
时, ,
,
∴函数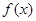 在
在 与
与 处都取得极值,∴
处都取得极值,∴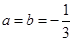 6分;
6分;
(2)由(1)知:函数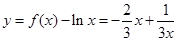 在
在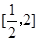 上递减,
上递减,
∴ 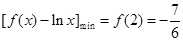 8分
8分
又 ∵函数 图象的对称轴是
图象的对称轴是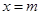 ,
,
①:当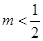 时:
时: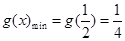 ,显然有
,显然有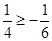 成立, ∴
成立, ∴ 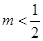 ,
,
②:当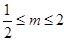 时:
时: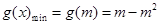 ,∴
,∴ , 解得:
, 解得: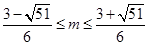 ,
,
又∵ 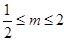 ,∴
,∴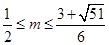 .
.
③:当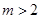 时:
时: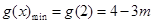 ,∴
,∴ 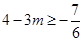 , ∴
, ∴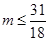 , 又
, 又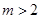 ,∴
,∴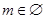
综上所述: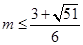 12分,
12分,
∴实数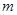 的取值范围为
的取值范围为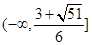 &nbs
&nbs

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
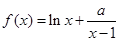 在
在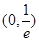 内有极值.
内有极值. 的取值范围;
的取值范围;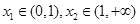 求证:
求证: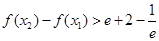 .
.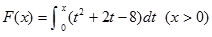 .
. 的单调区间;(2)求函数
的单调区间;(2)求函数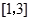 上的最值.
上的最值.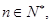 圆
圆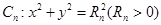 与
与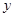 轴正半轴的交点为
轴正半轴的交点为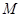 ,与曲线
,与曲线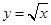 的交点为
的交点为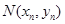 ,直线
,直线 与
与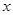 轴的交点为
轴的交点为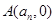 .
. 表示
表示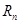 和
和
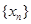 满足
满足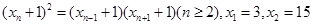
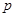 的值,使得数列
的值,使得数列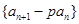 成等比数列;
成等比数列;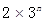 的大小.
的大小. (a∈R).
(a∈R).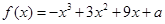 ,
,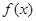 的单调递减区间;
的单调递减区间;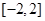 上的最大值为20,求它在该区间上的最小值.
上的最大值为20,求它在该区间上的最小值. 平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为
平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为 元.
元.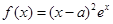 在
在 时取得极小值.
时取得极小值. 的值;
的值;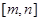 ,使得
,使得 在该区间上的值域为
在该区间上的值域为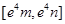 ?若存在,求出
?若存在,求出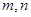 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. .
. 的单调性;
的单调性; ,证明:
,证明: .
.