题目内容
某地一渔场的水质受到了污染.渔场的工作人员对水质检测后,决定往水中投放一种药剂来净化水质. 已知每投放质量为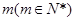 个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中
个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中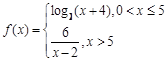 ,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.
,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.
(1)如果投放的药剂质量为m=6,试问渔场的水质达到有效净化一共可持续几天?
(2)如果投放的药剂质量为m,为了使在8天(从投放药剂算起包括第8天)之内的渔场的水质达到最佳净化,试确定应该投放的药剂质量m的取值范围.
(1)8天;(2)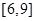
解析试题分析:(1)由已知得,经过x天该药剂在水中释放的浓度 y=mf(x)是关于自变量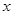 的分段函数,渔场的水质达到有效净化,只需
的分段函数,渔场的水质达到有效净化,只需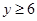 ,当m=6时,
,当m=6时,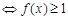 ,相当于知道函数值的取值范围,求自变量
,相当于知道函数值的取值范围,求自变量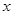 的取值范围,即可持续的天数确定;(2)由题意知,为了使在8天(从投放药剂算起包括第8天)之内的渔场的水质达到最佳净化,只需在这8天内的每一天均有
的取值范围,即可持续的天数确定;(2)由题意知,为了使在8天(从投放药剂算起包括第8天)之内的渔场的水质达到最佳净化,只需在这8天内的每一天均有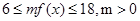 恒成立即可,转化为求分段函数求值域问题,使其含于
恒成立即可,转化为求分段函数求值域问题,使其含于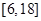 即可.
即可.
(1)由题设:投放的药剂质量为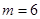 ,渔场的水质达到有效净化
,渔场的水质达到有效净化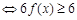
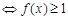
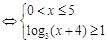 或
或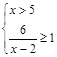
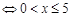 或
或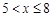 ,即:
,即: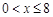 ,
,
所以如果投放的药剂质量为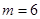 ,自来水达到有效净化一共可持续8天 . 6分
,自来水达到有效净化一共可持续8天 . 6分
(2)由题设: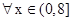 ,
,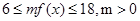 ,∵
,∵ ,
,
∴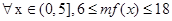 ,且
,且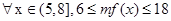 ,
,
∴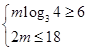 且
且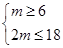 ,所以
,所以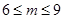 ,投放的药剂质量m的取值范围为
,投放的药剂质量m的取值范围为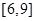 .
.
考点:分段函数.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数 .
. 的值,并解释其实际意义;
的值,并解释其实际意义; ,现有
,现有 单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.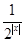 +2.
+2.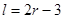 (
(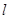 为圆柱的高,
为圆柱的高,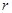 为球的半径,
为球的半径,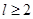 ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为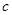 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.
 ,其中a为大于零的常数.
,其中a为大于零的常数. +
+ +…+
+…+ 恒成立.
恒成立. 
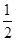 )时恒成立,求实数a的取值范围.
)时恒成立,求实数a的取值范围.