题目内容
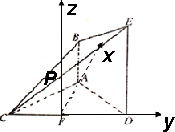
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.

(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)求平面BCE与平面ACD所成锐二面角的大小.
答案:
解析:
解析:
|
解:(1)解:取CE中点P,连结FP、BP, ∵F为CD的中点,∴FP∥DE,且FP= 又AB∥DE,且AB= ∴ABPF为平行四边形,∴AF∥BP. 2分 又∵AF ∴AF∥平面BCE. 4分 (2)∵△ACD为正三角形,∴AF⊥CD ∵AB⊥平面ACD,DE∥AB, ∴DE⊥平面ACD,又AF ∴DE⊥AF.又AF⊥CD,CD∩DE=D, ∴AF⊥平面CDE. 6分 又BP∥AF,∴BP⊥平面CDE.又∵BP ∴平面BCE⊥平面CDE. 8分 (3)法一、由(2),以F为坐标原点, FA,FD,FP所在的直线分别为x,y,z轴(如图),
建立空间直角坐标系F-xyz.设AC=2, 则C(0,-1,0), 显然, 设面BCE与面ACD所成锐二面角为 则 即平面BCE与平面ACD所成锐二面角为45°. 14分 法二、延长EB、DA,设EB、DA交于一点O,连结CO.
则 由AB是 在 即平面BCE与平面ACD所成锐二 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 11分
11分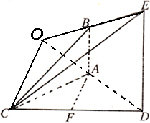
 (2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
(2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点. (2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点 如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.