题目内容
若曲线|x|+|y|=2和圆x2+y2=r2(r>0)没有公共点,则r的取值范围是
- A.r>2
- B.r<2
- C.

- D.
 或r>2
或r>2
D
分析:依题意可作出曲线|x|+|y|=2和圆x2+y2=r2(r>0),利用圆心到直线的距离公式判断即可.
解答:∵曲线|x|+|y|=2和圆x2+y2=r2(r>0)没有公共点,
作出曲线|x|+|y|=2和圆x2+y2=r2(r>0)的图形如下:

由图可知,圆心O(0,0)到曲线|x|+|y|=2的距离d=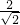 =
= ,
,
∴当d>r(曲线|x|+|y|=2和圆x2+y2=r2(r>0)相离)
或d<r(圆x2+y2=r2(r>0)含曲线|x|+|y|=2(两虚圆之间的四条线段))时,曲线|x|+|y|=2和圆x2+y2=r2(r>0)没有公共点,
∴r< 或r>2.
或r>2.
故选D.
点评:本题考查直线与圆的位置关系考查圆心到直线的距离公式,作出两曲线的图形是难点,也是分析的关键,属于中档题.
分析:依题意可作出曲线|x|+|y|=2和圆x2+y2=r2(r>0),利用圆心到直线的距离公式判断即可.
解答:∵曲线|x|+|y|=2和圆x2+y2=r2(r>0)没有公共点,
作出曲线|x|+|y|=2和圆x2+y2=r2(r>0)的图形如下:

由图可知,圆心O(0,0)到曲线|x|+|y|=2的距离d=
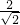 =
= ,
,∴当d>r(曲线|x|+|y|=2和圆x2+y2=r2(r>0)相离)
或d<r(圆x2+y2=r2(r>0)含曲线|x|+|y|=2(两虚圆之间的四条线段))时,曲线|x|+|y|=2和圆x2+y2=r2(r>0)没有公共点,
∴r<
 或r>2.
或r>2.故选D.
点评:本题考查直线与圆的位置关系考查圆心到直线的距离公式,作出两曲线的图形是难点,也是分析的关键,属于中档题.

练习册系列答案
相关题目

 或r>2
或r>2 的形式,称之为二行二列矩阵,定义矩阵的一种运算
的形式,称之为二行二列矩阵,定义矩阵的一种运算 •
• =
= ,该运算的几何意义为平面上的点(x,y)在矩阵
,该运算的几何意义为平面上的点(x,y)在矩阵 的作用下变换成点(ax+by,cx+dy),则若曲线x+y=1在矩阵
的作用下变换成点(ax+by,cx+dy),则若曲线x+y=1在矩阵 的作用下变换成曲线2x-y=1,则a+b的值为 .
的作用下变换成曲线2x-y=1,则a+b的值为 .