题目内容
已知集合 ,集合B={x|log4(x+1)<a},且A∩B=∅,则a的取值范围是________.
,集合B={x|log4(x+1)<a},且A∩B=∅,则a的取值范围是________.
a≤1
分析:先把集合A中不等式的右边的1化为20,由2大于1,得到指数函数为增函数,进而根据指数的大小得到关于x的不等式,求出不等式的解集确定出集合A,然后再把集合B中不等式的右边变形,根据4大于1,得到对数函数为增函数,同理可得关于x的不等式,求出不等式的解集可得到集合B,由两集合的交集为空集,列出关于a的不等式,求出不等式的解集得到满足题意的a的范围.
解答:由集合A中的不等式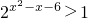 =20,
=20,
由2>1,得到指数函数为增函数,
∴x2-x-6>0,即(x-3)(x+2)>0,
解得:x>3或x<-2,
∴集合A={x|x>3或x<-2};
又对数函数为增函数,
由log4(x+1)<a=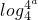 ,得到x+1<4a,即x<4a-1,
,得到x+1<4a,即x<4a-1,
由集合B中的不等式左边的对数函数y=log4(x+1),且A∩B=∅,
得到-1<x≤3,
∴4a-1≤3,解得a≤1,
则a的取值范围是a≤1.
故答案为:a≤1
点评:此题属于以指数函数及对数函数的单调性及特殊点为平台,考查了交集的运算,熟练掌握指数及对数函数的性质是解本题的关键.
分析:先把集合A中不等式的右边的1化为20,由2大于1,得到指数函数为增函数,进而根据指数的大小得到关于x的不等式,求出不等式的解集确定出集合A,然后再把集合B中不等式的右边变形,根据4大于1,得到对数函数为增函数,同理可得关于x的不等式,求出不等式的解集可得到集合B,由两集合的交集为空集,列出关于a的不等式,求出不等式的解集得到满足题意的a的范围.
解答:由集合A中的不等式
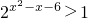 =20,
=20,由2>1,得到指数函数为增函数,
∴x2-x-6>0,即(x-3)(x+2)>0,
解得:x>3或x<-2,
∴集合A={x|x>3或x<-2};
又对数函数为增函数,
由log4(x+1)<a=
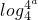 ,得到x+1<4a,即x<4a-1,
,得到x+1<4a,即x<4a-1,由集合B中的不等式左边的对数函数y=log4(x+1),且A∩B=∅,
得到-1<x≤3,
∴4a-1≤3,解得a≤1,
则a的取值范围是a≤1.
故答案为:a≤1
点评:此题属于以指数函数及对数函数的单调性及特殊点为平台,考查了交集的运算,熟练掌握指数及对数函数的性质是解本题的关键.

练习册系列答案
相关题目