题目内容
如图,四边形ABCD被两条对角线分成四个小三角形,现有4种不同颜色将它染色,使相邻三角形均不同色,求使△AOB与△COD 同色且△BOC与△AOD也同色的概率( )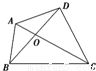
A.

B.

C.

D.

【答案】分析:根据题意结合排列组合有关公式,分别算出所有的涂色方案和△AOB与△COD同色且△BOC与△AOD也同色的涂色方案,再用古典概型计算公式加以计算即可得到本题所求的概率.
解答:解:根据题意,所有涂色的方案为
①若△AOB与△COD同色,它们共有4种涂法,对每一种涂法,△BOC与△AOD各有3种涂法,
此时共有4×3×3=36 种涂法.
②若△AOB与△COD不同色,它们共有4×3=12 种涂法,
对每一种涂法△BOC与△AOD各有2种涂法,此时有4×3×2×2=48(种)涂法.
因此,总共有36+48=84种不同的涂色方案;
而△AOB与△COD同色且△BOC与△AOD也同色的涂色方案有C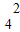 •A
•A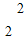 =12
=12
因此,使△AOB与△COD 同色且△BOC与△AOD也同色的概率为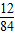 =
=
故选:C
点评:本题给出涂色问题,求对顶的两组三角形颜色均相同的概率.着重考查了排列组合的公式、原理和古典概型计算公式等知识,属于中档题.
解答:解:根据题意,所有涂色的方案为
①若△AOB与△COD同色,它们共有4种涂法,对每一种涂法,△BOC与△AOD各有3种涂法,
此时共有4×3×3=36 种涂法.
②若△AOB与△COD不同色,它们共有4×3=12 种涂法,
对每一种涂法△BOC与△AOD各有2种涂法,此时有4×3×2×2=48(种)涂法.
因此,总共有36+48=84种不同的涂色方案;
而△AOB与△COD同色且△BOC与△AOD也同色的涂色方案有C
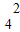 •A
•A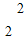 =12
=12因此,使△AOB与△COD 同色且△BOC与△AOD也同色的概率为
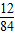 =
=
故选:C
点评:本题给出涂色问题,求对顶的两组三角形颜色均相同的概率.着重考查了排列组合的公式、原理和古典概型计算公式等知识,属于中档题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD.
如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD. 如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB= 如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点.
如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点. 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=