题目内容
(选做)
设关于x的二次函数f(x)=anx2-6an+1x+2(n∈N*)的图象与x轴交于两点(α,0),(β,0),且满足α-αβ+β=3.
(I)试用an表示an+1;
(II)当a1=
时,求数列{an}的通项公式.
设关于x的二次函数f(x)=anx2-6an+1x+2(n∈N*)的图象与x轴交于两点(α,0),(β,0),且满足α-αβ+β=3.
(I)试用an表示an+1;
(II)当a1=
| 7 | 6 |
分析:(I)根据韦达定理,得α+β=
,αβ=
,代入α-αβ+β=3.即可得出用an表示an+1的关系式.
(II)由(I)求出an+1-
=
an-
=
(an-
),构造出数列{an-
}是公比为
的等比数列,通过求出数列{an-
}的通项公式求出数列{an}的通项公式.
| 6an+1 |
| an |
| 2 |
| an |
(II)由(I)求出an+1-
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
解答:解:(I)根据韦达定理,得α+β=
,αβ=
由α-αβ+β=3
得6•
-
=3
故an+1=
an+
(3分)
(II)因为an+1-
=
an-
=
(an-
)
所以
=
所以数列{an-
}是公比为
的等比数列(8分)
因为当a1=
时,a1-
=
所以数列{an-
}的通项公式an-
=
•(
)n-1
故数列{an}的通项公式为an=
+
(10分)
| 6an+1 |
| an |
| 2 |
| an |
由α-αβ+β=3
得6•
| an+1 |
| an |
| 2 |
| an |
故an+1=
| 1 |
| 2 |
| 1 |
| 3 |
(II)因为an+1-
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
所以
an+1-
| ||
an-
|
| 1 |
| 2 |
所以数列{an-
| 2 |
| 3 |
| 1 |
| 2 |
因为当a1=
| 7 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
所以数列{an-
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
故数列{an}的通项公式为an=
| 2 |
| 3 |
| 1 |
| 2n |
点评:本题主要考查数列的递推公式、通项公式求解,考查转化构造、推理计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:
A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是: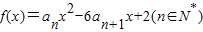 的图象与x轴交于两点(α,0),(β,0),且满足α-αβ+β=3.
的图象与x轴交于两点(α,0),(β,0),且满足α-αβ+β=3. 时,求数列{an}的通项公式.
时,求数列{an}的通项公式.