题目内容

设函数f(x)=2|x+1|-|x-1|,求使f(x)≥的x的取值范围.

解析:f(x)≥2|x+1|-|x-1|≥.

∵函数y=2x在(-∞,+∞)上单调递增,

∴|x+1|-|x-1|≥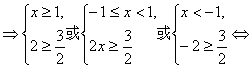x≥1或≤x＜1.

∴x≥.

∴x的取值范围为［,+∞).

练习册系列答案
相关题目
设函数f(x)=
2-xx∈(-∞，1)
x2x∈[1，+∞)
若f（x）＞4，则x的取值范围是
 
．
设函数f(x)=2
-x2+x+2
，对于给定的正数K，定义函数fK(x)=
f(x)，f(x)≤K
K，f(x)＞K
若对于函数f(x)=2
-x2+x+2
定义域内的任意 x，恒有fK（x）=f（x），则（　　）
A、K的最大值为2
2
B、K的最小值为2
2
C、K的最大值为1
D、K的最小值为1
（2011•渭南三模）设函数f(x)=
-2，x＞0
x2+bx+c，x≤0
若f（-4）=f（0），f（-2）=0，则关于x的不等式f（x）≤1的解集为（　　）
设函数f(x)=
2-x，x＜1
log4x，   x＞1
，满足f(x)=
1
4
的x的值为
2
2
．
已知：向量
m
=(sinx，
3
4
)，
n
=(cosx，-1)，设函数f(x)=2(
m
+
n
)•
n

（1）求f（x）解析式；
（2）在△ABC中，内角A，B，C的对边分别为a，b，c．若a=
3
，b=2，sinB=
6
3
，求f(x)+4cos(2A+
π
6
) (x∈[0，
π
2
])的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网