题目内容
已知函数f(x)= sin(2x+
sin(2x+ )
)
(1)若将函数y=f(x)的图象向左平移a(a>0)个单位长度得到的图象恰好关于点( ,0)对称,求实数a的最小值;
,0)对称,求实数a的最小值;
(2)若函数y=f(x)在[ ,
, π](b∈N*)上为减函数,试求实数b的值.
π](b∈N*)上为减函数,试求实数b的值.
解:(1)将函数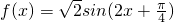 的图象,
的图象,
向左平移a个单位长度得到函数
 =
=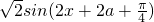 的图象.(2分)
的图象.(2分)
∵函数 的图象关于点
的图象关于点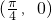 对称,
对称,
∴ ,∴
,∴ .
.
∵a>0∴ .
.
∵k∈Z,∴当k=1时, .(6分)
.(6分)
(2)∵
在 (b∈N*)上为减函数,
(b∈N*)上为减函数,
又 的递减区间为
的递减区间为
 k∈Z,
k∈Z,
∴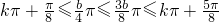 .(8分)
.(8分)
∴ .
.
由 ,得k≤
,得k≤ .
.
又b∈N*,∴k只能取0.∴ ,b=1.(12分)
,b=1.(12分)
分析:(1)求出函数y=f(x)的图象向左平移a(a>0)个单位长度得到的解析式,利用x= 时函数值为0,求出a的表达式,然后求出最小值.
时函数值为0,求出a的表达式,然后求出最小值.
(2)求出函数的单调减区间,[ ,
, π]是减区间的子集,得到不等式组,求出实数b的值.
π]是减区间的子集,得到不等式组,求出实数b的值.
点评:本题是中档题,考查三角函数的基本性质,函数图象的平移,奇偶性、单调性,考查分析问题解决问题的能力,集合的基本关系.
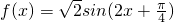 的图象,
的图象,向左平移a个单位长度得到函数
 =
=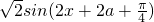 的图象.(2分)
的图象.(2分)∵函数
 的图象关于点
的图象关于点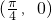 对称,
对称,∴
 ,∴
,∴ .
.∵a>0∴
 .
.∵k∈Z,∴当k=1时,
 .(6分)
.(6分)(2)∵

在
 (b∈N*)上为减函数,
(b∈N*)上为减函数,又
 的递减区间为
的递减区间为 k∈Z,
k∈Z,∴
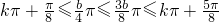 .(8分)
.(8分)∴
 .
.由
 ,得k≤
,得k≤ .
.又b∈N*,∴k只能取0.∴
 ,b=1.(12分)
,b=1.(12分)分析:(1)求出函数y=f(x)的图象向左平移a(a>0)个单位长度得到的解析式,利用x=
 时函数值为0,求出a的表达式,然后求出最小值.
时函数值为0,求出a的表达式,然后求出最小值.(2)求出函数的单调减区间,[
 ,
, π]是减区间的子集,得到不等式组,求出实数b的值.
π]是减区间的子集,得到不等式组,求出实数b的值.点评:本题是中档题,考查三角函数的基本性质,函数图象的平移,奇偶性、单调性,考查分析问题解决问题的能力,集合的基本关系.

练习册系列答案
相关题目
