Question

（本小题满分15分）

某广场一雕塑造型结构如图所示，最上层是一呈水平状态的圆环，其半径为，通过金属杆支撑在地面处（垂直于水平面），是圆环上的三等分点，圆环所在的水平面距地面，设金属杆所在直线与圆环所在水平面所成的角都为。（圆环及金属杆均不计粗细）

（1）当的正弦值为多少时，金属杆的总长最短？

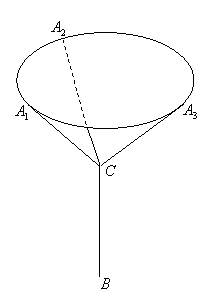（2）为美观与安全，在圆环上设置个等分点，并仍按上面方法连接，若还要求金属杆的总长最短，对比（1）中点位置，此时点将会上移还是下移，请说明理由。

Answer 1

解：（Ⅰ）设为圆环的圆心，依题意，∠CA₁O=∠CA₂O=∠CA₃O=，

CA₁=CA₂=CA₃=，CO=，

设金属杆总长为ym，则

=，（）

，

当时，；当时，，

∴当时，函数有极小值，也是最小值。     ……………………………………7分

（Ⅱ）依题意，=，

，

当时，；当时，，

∴当时，函数有极小值，也是最小值。…………………………………………13分

当n≥4时，，所以C点应上移。        …………………………………………15分