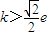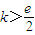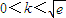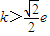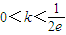Question

已知k＞0，函数f(x)=x3-3x+k，g(x)=

2kx-k

x2+2

（1）若对任意x₁，x₂∈[-1，1]都有f（x₁）≥g（x₂），求k的取值范围；
（2）若存在x₁，x₂∈[-1，1]，使得f（x₁）＜g（x₂），求k的取值范围．

Answer 1

分析：（1）对任意x₁，x₂∈[-1，1]都有f（x₁）≥g（x₂），等价于f（x）_min≥g（x）_max，进而转化为函数的最值问题；
（2）存在x₁，x₂∈[-1，1]，使得f（x₁）＜g（x₂），等价于f（x）_min＜g（x）_max，进而转化为函数的最值问题．

解答：解：（1）f′（x）=3x²-3=3（x+1）（x-1），
当x∈[-1，1]时，f′（x）≤0，所以f（x）在[-1，1]上单调递减，f（x）_min=f（1）=k-2；
g′（x）=

-2k(x2-x-2)

(x2+2)2

=

-2k(x-2)(x+1)

(x2+2)2

，
当x∈[-1，1]时，g′（x）≥0，所以g（x）在[-1，1]上单调递增，g（x）_max=g（1）=

k

3

．
对任意x₁，x₂∈[-1，1]都有f（x₁）≥g（x₂），等价于f（x）_min≥g（x）_max，
即k-2≥

k

3

，解得k≥3．
所以k的取值范围是[3，+∞）．
（2）由（1）知：f（x）在[-1，1]上单调递减，f（x）_min=f（1）=k-2；
g（x）在[-1，1]上单调递增，g（x）_max=g（1）=

k

3

．
存在x₁，x₂∈[-1，1]，使得f（x₁）＜g（x₂），等价于f（x）_min＜g（x）_max，
即k-2＜

k

3

，解得0＜k＜3．
所以k的取值范围是（0，3）．

点评：本题为不等式恒成立问题，解决的基本思路是转化为函数最值问题处理，从而可用导数解决．本题注意分析两问间的“否定”关系．