Question

将地球看作半径为R的球，在北纬45⁰圈上有A、B两地，且A地在东经30⁰线上，B地在西经60⁰线上．现要在A、B两地间开辟一条航道，则航道的最短长度为（　　）

• A．

  π

  6

  R
• B．

  π

  3

  R
• C．

  π

  2

  R
• D．πR

Answer 1

分析：欲求坐飞机从A城市飞到B城市的最短距离，即求出地球上这两点间的球面距离即可．A、B两地在同一纬度圈上，计算经度差，求出AB弦长，以及球心角，然后求出球面距离．即可得到答案．

解答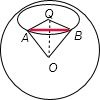：解：由已知地球半径为R，
则北纬45°的纬线圈半径为

2

2

R
又∵两座城市的经度分别为东经30°和西经60°
故连接两座城市的弦长L=

2

2

R•

2

=R
则A，B两地与地球球心O连线的夹角∠AOB=

π

3

则A、B两地之间的距离是

π

3

R
故选B．

点评：本题考查球面距离及解三角形计算，考查空间想象能力，是基础题．