题目内容
已知函数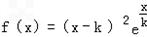 .
.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若对于任意的x∈(0,+∞),都有f(x)≤ ,求k的取值范围.
,求k的取值范围.
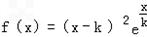 .
.(Ⅰ)求f(x)的单调区间;
(Ⅱ)若对于任意的x∈(0,+∞),都有f(x)≤
 ,求k的取值范围.
,求k的取值范围.解:(Ⅰ)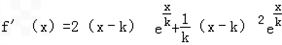 =
=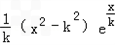 ,
,
令f'(x)=0,得x=±k
当k>0时,f'(x)f(x)随x的变化情况如下:
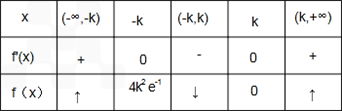
所以,f(x)的单调递增区间是(﹣∞,﹣k),和(k,+∞),
单调递减区间是(﹣k,k);
当k<0时,f'(x)f(x)随x的变化情况如下:
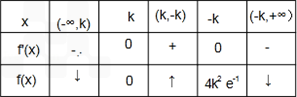
所以,f(x)的单调递减区间是(﹣∞,k),和(﹣k,+∞),
单调递增区间是(k,﹣k);
(Ⅱ)当k>0时,∵f(k+1)=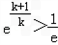 ,
,
∴有任意的x∈(0,+∞),都有f(x)≤ ,
,
当k<0时,由(I)知f(x)在(0,+∞)上的最大值是f(﹣k)=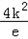 ,
,
∴任意的x∈(0,+∞),f(x)≤ ,
, f(﹣k)=
f(﹣k)=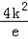 ≤
≤ ,
,
解得﹣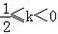 ,
,
故对于任意的x∈(0,+∞),都有f(x)≤ ,k的取值范围是﹣
,k的取值范围是﹣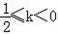 .
.
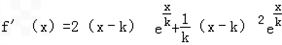 =
=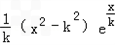 ,
,令f'(x)=0,得x=±k
当k>0时,f'(x)f(x)随x的变化情况如下:

所以,f(x)的单调递增区间是(﹣∞,﹣k),和(k,+∞),
单调递减区间是(﹣k,k);
当k<0时,f'(x)f(x)随x的变化情况如下:

所以,f(x)的单调递减区间是(﹣∞,k),和(﹣k,+∞),
单调递增区间是(k,﹣k);
(Ⅱ)当k>0时,∵f(k+1)=
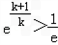 ,
,∴有任意的x∈(0,+∞),都有f(x)≤
 ,
,当k<0时,由(I)知f(x)在(0,+∞)上的最大值是f(﹣k)=
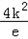 ,
,∴任意的x∈(0,+∞),f(x)≤
 ,
, f(﹣k)=
f(﹣k)=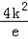 ≤
≤ ,
,解得﹣
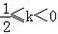 ,
,故对于任意的x∈(0,+∞),都有f(x)≤
 ,k的取值范围是﹣
,k的取值范围是﹣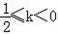 .
.
练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 .
. .
. 个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值. .
. 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围. .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值. .
.