题目内容
若点O和点F分别为椭圆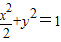 的中心和右焦点,点P为椭圆上的任意一点,则
的中心和右焦点,点P为椭圆上的任意一点,则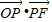 的最大值为 .
的最大值为 .
【答案】分析:先求出左焦点坐标F,设P(x,y),根据P(x,y)在椭圆上可得到x、y的关系式,表示出向量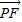 、
、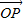 ,根据数量积的运算将x、y的关系式代入组成二次函数进而可确定答案.
,根据数量积的运算将x、y的关系式代入组成二次函数进而可确定答案.
解答:解:由题意,F(1,0),设点P(x,y),则有 ,解得
,解得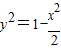 ,
,
因为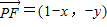 ,
,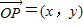 ,
,
所以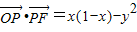 =x(1-x)-
=x(1-x)-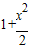 =
=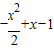 ,
,
此二次函数对应的抛物线的对称轴为x=1,
因为-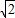 ≤x≤
≤x≤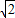 ,所以当x=1时,则
,所以当x=1时,则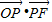 的最大值为
的最大值为 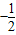 .
.
故答案为: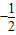 .
.
点评:本题考查椭圆的方程、几何性质、平面向量的数量积的坐标运算、二次函数的单调性与最值等,考查了同学们对基础知识的熟练程序以及知识的综合应用能力、运算能力.
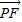 、
、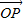 ,根据数量积的运算将x、y的关系式代入组成二次函数进而可确定答案.
,根据数量积的运算将x、y的关系式代入组成二次函数进而可确定答案.解答:解:由题意,F(1,0),设点P(x,y),则有
 ,解得
,解得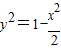 ,
,因为
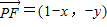 ,
,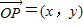 ,
,所以
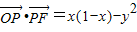 =x(1-x)-
=x(1-x)-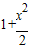 =
=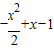 ,
,此二次函数对应的抛物线的对称轴为x=1,
因为-
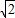 ≤x≤
≤x≤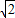 ,所以当x=1时,则
,所以当x=1时,则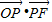 的最大值为
的最大值为 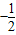 .
.故答案为:
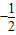 .
.点评:本题考查椭圆的方程、几何性质、平面向量的数量积的坐标运算、二次函数的单调性与最值等,考查了同学们对基础知识的熟练程序以及知识的综合应用能力、运算能力.

练习册系列答案
相关题目
 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则
 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则 的最大值为
的最大值为 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则 的最大值为 (
)
的最大值为 (
)
 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则 的最大值为
的最大值为