题目内容
【题目】如图,在三棱柱![]() 中,
中, ![]() ,顶点
,顶点![]() 在底面
在底面 ![]() 上的射影恰为点
上的射影恰为点 ![]() ,且
,且![]() .
.

(1)求棱 ![]() 与
与![]() 所成的角的大小;
所成的角的大小;
(2)在棱 ![]() 上确定一点
上确定一点![]() ,使
,使![]() ,并求出二面角
,并求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:根据题意建立如图所示的空间直角坐标系,(1)求出![]() 与
与![]() ,所在直线的向量,利用向量的夹角公式即可求出结果,再根据异面直线成角的范围,即可求出结果;(2)平面
,所在直线的向量,利用向量的夹角公式即可求出结果,再根据异面直线成角的范围,即可求出结果;(2)平面![]() 和平面
和平面![]() 的法向量分别为m和n,即可求出二面角
的法向量分别为m和n,即可求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
试题解析:解(1)建立如图所示的空间直角坐标系,
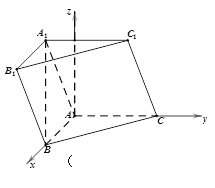
则C(0, 2, 0),B(2, 0 , 0),A1(0,-2, 2),B1(4, 0 , 2).从而, ![]() =(0,-2, 2),
=(0,-2, 2),![]() =(-2, 2, 0).
=(-2, 2, 0).
记![]() 与
与![]() 的夹角为θ,则有
的夹角为θ,则有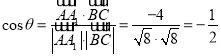 .
.
又由异面直线AA1与BC所成角的范围为(0,π),可得异面直线AA1与BC所成的角
为60. 4分
(2)记平面![]() 和平面
和平面![]() 的法向量分别为m和n,则由题设可令m=(x, y, z),且有平面
的法向量分别为m和n,则由题设可令m=(x, y, z),且有平面![]() 的法向量为n=(0,2,0).
的法向量为n=(0,2,0).
设![]() =(-2λ, 2λ, 0),则P(4-2λ, 2λ, 2).
=(-2λ, 2λ, 0),则P(4-2λ, 2λ, 2).
于是AP=![]() ,解得λ=
,解得λ=![]() 或λ=
或λ=![]() .
.
又题设可知λ∈(0, 1),则λ=![]() 舍去,故有λ=
舍去,故有λ=![]() .
.
从而,P为棱![]() 的中点,则坐标为P(3, 1, 2).
的中点,则坐标为P(3, 1, 2).
由平面PAB的法向量为m,故m⊥![]() 且m⊥
且m⊥![]() .
.
由m·![]() =0,即(x, y, z)·(3, 1 ,2)=0,解得3x+y+2z=0; ①
=0,即(x, y, z)·(3, 1 ,2)=0,解得3x+y+2z=0; ①
由m·![]() =0,即(x, y, z)·(-1,-1,-2)=0,解得-x-y-2z=0,②
=0,即(x, y, z)·(-1,-1,-2)=0,解得-x-y-2z=0,②
解方程①、②可得,x=0,y+2z=0,令y=-2,z=1,
则有m=(0,-2, 1) .
记平面PAB和平面ABA1所成的角为β,
则cosβ=![]() =
=![]()
故二面角![]() 的平面角的余弦值是
的平面角的余弦值是![]() .
.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目