题目内容
(2012•通州区一模)已知在△ABC中,A=
,sinC=
,BC=3,那么AB=
;AC=
.
| π |
| 3 |
| ||
| 2 |
| 6 |
| 6 |
| ||||
| 2 |
| ||||
| 2 |
分析:根据正弦定理,结合题中的数据可直接计算出AB的长.根据两角和的正弦公式和三角形内角和定理,计算出sinB的值,再用一次正弦定理,可算出AC的长.
解答:解:∵
=BCsinA,
∴AB=
=
=
∵A+B+C=π,
∴sinB=sin(A+C)=
×
+
×
=
,
由此可得:AC=
=
故答案为:
;
| AB |
| sinC |
∴AB=
| BCsinC |
| sinA |
3×
| ||||
| sin60° |
| 6 |
∵A+B+C=π,
∴sinB=sin(A+C)=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||||
| 4 |
由此可得:AC=
| ABsinB |
| sinC |
| ||||
| 2 |
故答案为:
| 6 |
| ||||
| 2 |
点评:本题给出三角形一边长和两个内角的大小,求另外两条边的长度,着重考查了正弦定理、正弦的诱导公式和两角和的正弦公式等知识点,属于基础题.

练习册系列答案
相关题目
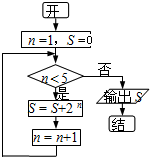 (2012•通州区一模)如图,程序框图所进行的求和运算是( )
(2012•通州区一模)如图,程序框图所进行的求和运算是( )