题目内容

设一个球的表面积为S₁，它的内接正方体的表面积为S₂，则 $数学公式$ 的值等于

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

D
分析：设出正方体的棱长，然后求出正方体的表面积，求出正方体的体对角线的长，就是球的直径，求出球的表面积，即可得到二者的比值．
解答：设正方体的棱长为：1，
所以正方体的表面积为：S₂=6；
正方体的体对角线的长为： $\text{[math]}$ ，就是球的直径，
所以球的表面积为：S₁= $\text{[math]}$ =3π．
所以 $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．
故选D．
点评：本题考查球的体积表面积，正方体的外接球的知识，仔细分析，找出二者之间的关系：正方体的对角线就是球的直径，是解题关键，本题考查转化思想，是基础题．

练习册系列答案

寒假习训浙江教育出版社系列答案

寒假作业美妙假期云南科技出版社系列答案

归类加模拟考试卷新疆文化出版社系列答案

全程达标小升初模拟加真题考试卷新疆美术摄影出版社系列答案

中考方舟真题超详解系列答案

一品教育一品设计河南人民出版社系列答案

快乐假期行寒假用书系列答案

启航文化赢在假期寒假济南出版社系列答案

快乐假期智趣寒假花山文艺出版社系列答案

大联考期末复习合订本系列答案

相关题目

把一个半径为r的实心铁球O熔化铸成两个实心小球O₁与O₂，假设没有任何损耗、设铁球O的表面积为S，小球O₁的半径为r₁，表面积为S₁，小球O₂的半径为r₂，两个小球的半径之比r₁：r₂=1：2，那么球O₁的表面积与球O的表面积之比S₁：S=（　　）

3	3

把一个半径为r的实心铁球O熔化铸成两个实心小球O₁与O₂，假设没有任何损耗.设铁球O的表面积为S，小球O₁的半径为r₁，表面积为S₁，小球O₂的半径为r₂，两个小球的半径之比，那么球O₁的表面积与球O的表面积之比= .

把一个半径为r的实心铁球O熔化铸成两个实心小球O₁与O₂，假设没有任何损耗、设铁球O的表面积为S，小球O₁的半径为r₁，表面积为S₁，小球O₂的半径为r₂，两个小球的半径之比r₁：r₂=1：2，那么球O₁的表面积与球O的表面积之比S₁：S=（）
A．1：3
B．

C．1：5
D．1：9

把一个半径为r的实心铁球O熔化铸成两个实心小球O₁与O₂，假设没有任何损耗。设铁球O的表面积为S，小球O₁的半径为r₁，表面积为S₁，小球O₂的半径为r₂，两个小球的半径之比r₁：r₂=1：2，那么球O₁的表面积与球O的表面积之比S₁：S=（）。

把一个半径为r的实心铁球O熔化铸成两个实心小球O₁与O₂，假设没有任何损耗.设铁球O的表面积为S，小球O₁的半径为r₁，表面积为S₁，小球O₂的半径为r₂，两个小球的半径之比，那么球O₁的表面积与球O的表面积之比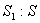= .