题目内容
不等式ax2+bx+c＞0（a，b，c∈Z）的解集为（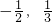
），则a+b的值可能为
- A.10
- B.-10
- C.14
- D.-14
D
分析：由不等式ax2+bx+c＞0（a，b，c∈Z）的解集为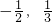（），可得a＜0，且
，解得b=
，又加之a，b，c∈Z，a只能为6的倍数，可知当a=-12时，b=-2，此时a+b=-14，可得答案．
解答：因为不等式ax2+bx+c＞0（a，b，c∈Z）的解集为（），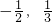
所以a＜0，且，
，解得b=，c=
由于a，b，c∈Z，b=，故a只能为6的倍数，当a=-12时，b=-2，
此时a+b=-14
故选D．
点评：本题为一元二次不等式的解集问题，注意解集的端点与对应一元二次方程的实根的关系，和a，b，c∈Z是解集问题的关键，属基础题．
分析：由不等式ax2+bx+c＞0（a，b，c∈Z）的解集为（
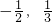），可得a＜0，且，解得b=，又加之a，b，c∈Z，a只能为6的倍数，可知当a=-12时，b=-2，此时a+b=-14，可得答案．解答：因为不等式ax2+bx+c＞0（a，b，c∈Z）的解集为（
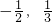），所以a＜0，且
，，解得b=，c=由于a，b，c∈Z，b=
，故a只能为6的倍数，当a=-12时，b=-2，此时a+b=-14
故选D．
点评：本题为一元二次不等式的解集问题，注意解集的端点与对应一元二次方程的实根的关系，和a，b，c∈Z是解集问题的关键，属基础题．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
下列结论正确的是（ ）
| A、不等式x2≥4的解集为{x|x≥±2} | ||||
| B、不等式x2-9＜0的解集为{x|x＜3} | ||||
C、不等式（x-1）2＜2的解集为{x|1-
| ||||
| D、设x1，x2为ax2+bx+c=0的两个实根，且x1＜x2，则不等式ax2+bx+c＜0的解集为{x|x1＜x＜x2} |