Question

已知数列{a_n}的前n项和为S_n=3n²-2n+1,问:此数列是否为等差数列?请说明理由.

Answer 1

思路分析:首先根据S_n求出a_n,然后利用等差数列的定义判断是否是等差数列.

    解:当n=1时,a₁=S₁=3×1²-2×1+1=2,

    当n≥2时,a_n=S_n-S_n-1=(3n²-2n+1)-［3(n-1)²-2(n-1)+1］=6n-5,

∴a_n=

    又当n≥2时,有a_n+1-a_n=［6(n+1)-5］-6n-5=6,

    而a₂-a₁=(6×2-5)-2=5≠6,∴此数列不是等差数列.

    思维启示:下面的解法是错的:∵a_n=S_n-S_n-1=(3n²-2n+1)-［3(n-1)²-2(n-1)+1］=6n-5(n∈N^*),

    又∵a_n+1-a_n=［6(n+1)-5］-(6n-5)=6,

∴{a_n}为等差数列.

    错因分析:①对公式a_n=S_n-S_n-1的成立条件不清,对已知S_n求a_n的方法不明.

公式a_n=S_n-S_n-1成立的条件是n∈N^*且n≥2,因此已知S_n求a_n的方法步骤为a_n=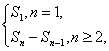再看n=1时,S_n-S_n-1是否等于S₁,以决定能否将a_n合并成一个式子.

②给出S_n判断一个数列是否是等差数列,首先根据S_n-S_n-1求出a_n(n≥2),若a₁符合a_n(n≥2),再判断是否是等差数列,否则{a_n}一定不是等差数列.

③数列{a_n}的前n项和是S_n,则{a_n}成等差数列的充要条件是S_n=an²+bn.