题目内容
【题目】已知函数![]() 在
在![]() 处有极值
处有极值![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)设![]() ,讨论函数
,讨论函数![]() 在区间
在区间![]() 上的单调性.
上的单调性.
【答案】(1) ![]() 在
在![]() 处有极值
处有极值![]() 时,
时,![]() ,(2)见解析.
,(2)见解析.
【解析】试题分析:(Ⅰ)求出导函数,由∴![]() 且
且![]() ,求得
,求得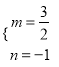 或
或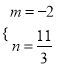 ,检验后可得结果;(Ⅱ)由(Ⅰ)可知
,检验后可得结果;(Ⅱ)由(Ⅰ)可知![]() ,利用导数研究函数的单调性和极值,分五种情况讨论,分别比较极值与端点处的函数值即可得结果.
,利用导数研究函数的单调性和极值,分五种情况讨论,分别比较极值与端点处的函数值即可得结果.
试题解析:(Ⅰ)![]() 定义域为
定义域为![]() ,
,
∵![]() 在
在![]() 处有极值
处有极值![]() ,
,
∴![]() 且
且![]() ,
,
即![]()
解得:![]() 或
或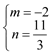
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
∴![]() 在
在![]() 处有极值
处有极值![]() 时,
时,![]() .
.
(Ⅱ)由(Ⅰ)可知![]() ,其单调性和极值分布情况如表:
,其单调性和极值分布情况如表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| 增 | 极大 | 减 | 极小 | 增 |
∴①当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上的单调递增;
上的单调递增;
②当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减;③当
上单调递减;③当![]() 且
且![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上单调递减;
上单调递减;
④当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上的单调递减,在区间
上的单调递减,在区间![]() 上单调递增;
上单调递增;
⑤![]() 时,
时,![]() 在区间
在区间![]() 上单调递增.
上单调递增.
综上所述,当![]() 时函数
时函数![]() 在区间
在区间![]() 上的单调性为:
上的单调性为:
![]() 或
或![]() 时,单调递增;
时,单调递增;
![]() 时,在
时,在![]() 上的单调递增,在
上的单调递增,在![]() 上单调递减;
上单调递减;
![]() 时,单调递减;
时,单调递减;
![]() 时,在
时,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
【方法点晴】本题主要考查的是利用导数研究函数的单调性、利用导数研究函数的极值与最值,属于难题.利用导数研究函数![]() 的单调性进一步求函数最值的步骤:①确定函数
的单调性进一步求函数最值的步骤:①确定函数![]() 的定义域;②对
的定义域;②对![]() 求导;③令
求导;③令![]() ,解不等式得
,解不等式得![]() 的范围就是递增区间;令
的范围就是递增区间;令![]() ,解不等式得
,解不等式得![]() 的范围就是递减区间;④根据单调性求函数
的范围就是递减区间;④根据单调性求函数![]() 的极值及最值(闭区间上还要注意比较端点处函数值的大小).
的极值及最值(闭区间上还要注意比较端点处函数值的大小).

【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 工人数(人) |
19 | 1 |
28 | 3 |
29 | 3 |
30 | 5 |
31 | 4 |
32 | 3 |
40 | 1 |
合计 | 20 |
(1)求这20名工人年龄的众数与极差;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)求这20名工人年龄的方差.
【题目】稳定房价是我国今年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响.北京市某房地产介绍所对本市一楼群在今年的房价作了统计与预测:发现每个季度的平均单价y(每平方米面积的价格,单位为元)与第x季度之间近似满足:y=500sin(ωx+)+9500 (>0),已知第一、二季度平均单价如下表所示:
x | 1 | 2 | 3 |
y | 10000 | 9500 | ? |
则此楼群在第三季度的平均单价大约是 ( )
A.10000元
B.9500元
C.9000元
D.8500元