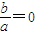题目内容
a,b∈R,则f(x)=x|sinx+a|+b是奇函数的充要条件是( )A.a2+b2=0
B.ab=0
C.
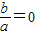
D.a2-b2=0
【答案】分析:由奇函数的性质得到f(0)=0,所以得到b=0,再结合奇函数的定义f(-x)=-f(x)解出a=0即可得到答案.
解答:解:因为函数的定义域为R,所以f(0)=0.
所以b=0.
所以f(x)=x|sinx+a|.
因为函数f(x)是奇函数,
所以f(-x)=-f(x)即-x|-sinx+a|=-x|sinx+a|,
所以|-sinx+a|=|sinx+a|,所以a=0.
故选A.
点评:解决此类问题的关键是熟练掌握奇函数的定义以及判断充要条件时实际就是解题的等价过程,充要条件的判断一般与其他知识相结合出现在选择题或填空题中.
解答:解:因为函数的定义域为R,所以f(0)=0.
所以b=0.
所以f(x)=x|sinx+a|.
因为函数f(x)是奇函数,
所以f(-x)=-f(x)即-x|-sinx+a|=-x|sinx+a|,
所以|-sinx+a|=|sinx+a|,所以a=0.
故选A.
点评:解决此类问题的关键是熟练掌握奇函数的定义以及判断充要条件时实际就是解题的等价过程,充要条件的判断一般与其他知识相结合出现在选择题或填空题中.

练习册系列答案
相关题目
a,b∈R,则f(x)=x|sinx+a|+b是奇函数的充要条件是( )
| A、a2+b2=0 | ||
| B、ab=0 | ||
C、
| ||
| D、a2-b2=0 |