题目内容
关于函数f(x)=cos(2x-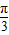 )+cos(2x+
)+cos(2x+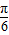 ),有下列命题:
),有下列命题:①y=f(x)的最大值为
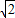 ;
;②y=f(x)是以π为最小正周期的周期函数;
③y=f(x)在区间(
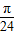 ,
,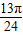 )上单调递减;
)上单调递减;④将函数y=
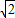 cos2x的图象向左平移
cos2x的图象向左平移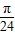 个单位后,将与已知函数的图象重合.
个单位后,将与已知函数的图象重合.其中正确命题的序号是 .(注:把你认为正确的命题的序号都填上)
【答案】分析:利用两角和差的正余弦公式可把f(x)化为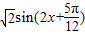 ,进而利用正弦函数的性质即可判断出答案.
,进而利用正弦函数的性质即可判断出答案.
解答:解:函数f(x)=cos(2x-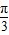 )+cos(2x+
)+cos(2x+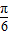 )=
)=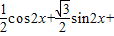
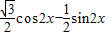
=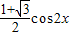
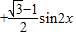 =
=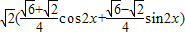 =
=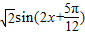 .
.
∴函数f(x)的最大值为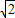 ,因此①正确;
,因此①正确;
周期T=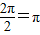 ,因此②正确;
,因此②正确;
当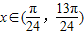 时,
时,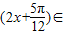
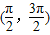 ,因此y=f(x)在区间(
,因此y=f(x)在区间(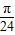 ,
,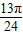 )上单调递减,因此③正确;
)上单调递减,因此③正确;
将函数y=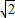 cos2x的图象向左平移
cos2x的图象向左平移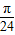 个单位后,得到y=
个单位后,得到y=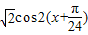
=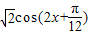 =
=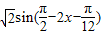 =
=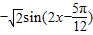
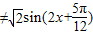 ,因此④不正确.
,因此④不正确.
综上可知:①②③.
故答案为①②③.
点评:熟练掌握两角和差的正余弦公式、正弦函数的性质是解题的关键.
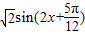 ,进而利用正弦函数的性质即可判断出答案.
,进而利用正弦函数的性质即可判断出答案.解答:解:函数f(x)=cos(2x-
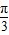 )+cos(2x+
)+cos(2x+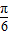 )=
)=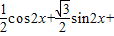
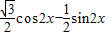
=
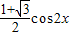
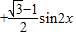 =
=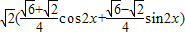 =
=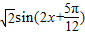 .
.∴函数f(x)的最大值为
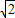 ,因此①正确;
,因此①正确;周期T=
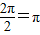 ,因此②正确;
,因此②正确;当
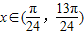 时,
时,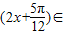
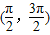 ,因此y=f(x)在区间(
,因此y=f(x)在区间(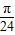 ,
,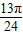 )上单调递减,因此③正确;
)上单调递减,因此③正确;将函数y=
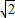 cos2x的图象向左平移
cos2x的图象向左平移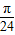 个单位后,得到y=
个单位后,得到y=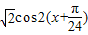
=
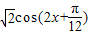 =
=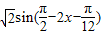 =
=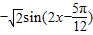
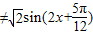 ,因此④不正确.
,因此④不正确.综上可知:①②③.
故答案为①②③.
点评:熟练掌握两角和差的正余弦公式、正弦函数的性质是解题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目