题目内容
2.已知函数f(x)=ax+1-ex(a∈R,e为自然对数的底数),若函数f(x)在点(1,f(1))处的切线平行于x轴,则a=e.分析 先求出函数的导数,得到f′(1)=a-e=0,解出即可.
解答 解:直线平行于x轴时斜率为0,
由f′(x)=a-ex,
得k=f′(1)=a-e=0,得出a=e,
故答案为:e.
点评 本题考查了导数的应用,考查曲线的切线问题,是一道基础题.

练习册系列答案
相关题目
17.函数f(x)=sin$\frac{2}{3}x+cos\frac{2}{3}$x的图象中相邻的两条对称轴间距离为( )
| A. | $\frac{3}{2}π$ | B. | $\frac{4}{3}π$ | C. | 3π | D. | $\frac{7}{6}π$ |
7.某中学高一(1)班有学生55人,现按座位号的编号采用系统抽样的方法选取5名同学参加一项活动,已知座位号为4号、15号、26号、48号的同学均被选出,则被选出的5名同学中还有一名的座位号是( )
| A. | 36 | B. | 37 | C. | 38 | D. | 39 |
11.在复平面内,复数i2(1-i)对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
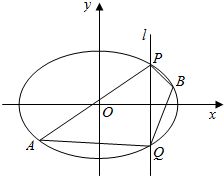 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,长轴长为4$\sqrt{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,长轴长为4$\sqrt{2}$.