题目内容
关于x的方程ex-1-|kx|=0(其中e=2.71828…是自然对数的底数)的有三个不同实根,则k的取值范围是
| A.{-2,0,2} | B.(1,+∞) | C.{k|k>e} | D.{k|k2>1} |
D
解析试题分析:由方程ex-1-|kx|=0得ex-1=|kx|,设函数f(x)=ex-1,g(x)=|kx|,然后分别作出函数f(x)和g(x)的图象,利用图象确定k的取值范围.
考点:(1)函数的图像与性质;(2)数形结合思想.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
若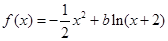 在
在 上是减函数,则
上是减函数,则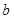 的取值范围是( )
的取值范围是( )
A.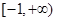 | B. | C.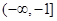 | D.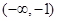 |
三个数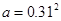 ,
, ,
,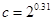 之间的大小关系( )
之间的大小关系( )
A.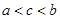 | B. | C. | D.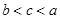 |
函数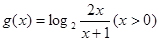 ,关于方程
,关于方程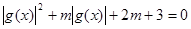 有三个不同实数解,则实数
有三个不同实数解,则实数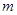 的取值范围为( )
的取值范围为( )
A.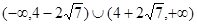 | B. |
C. | D.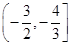 |
函数 的零点所在区间是( )
的零点所在区间是( )
A. | B. | C. | D. |
若定义在区间 上的函数
上的函数 满足:对于任意的
满足:对于任意的 ,都有
,都有 ,且
,且 时,有
时,有 ,
, 的最大值、最小值分别为
的最大值、最小值分别为 ,则
,则 的值为( )
的值为( )
| A.2012 | B.2013 | C.4024 | D.4026 |
已知 ,设函数
,设函数 的零点为
的零点为 ,
, 的零点为
的零点为 ,则
,则 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
已知f(x)=32x-(k+1)3x+2,当x∈R时,f(x)恒为正值,则k的取值范围是( )
| A.(-∞,-1) | B.(-∞,2 -1) -1) |
C.(-1,2 -1) -1) | D.(-2 -1,2 -1,2 -1) -1) |
 ,
, ,沿对角线AC折成如图所示的四面体,二面角B-AC-D为
,沿对角线AC折成如图所示的四面体,二面角B-AC-D为 ,M为AC的中点,P在线段DM上,记DP=x,PA+PB=y,则函数y=f(x)的图象大致为( )
,M为AC的中点,P在线段DM上,记DP=x,PA+PB=y,则函数y=f(x)的图象大致为( )
