题目内容
已知函数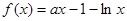
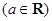 .
.
(Ⅰ)讨论函数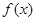 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(Ⅱ)若函数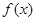 在
在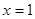 处取得极值,且对
处取得极值,且对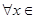
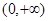 ,
,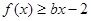 恒成立,
恒成立,
求实数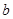 的取值范围;
的取值范围;
(Ⅲ)当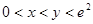 且
且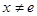 时,试比较
时,试比较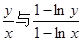 的大小。
的大小。
【答案】
(Ⅰ)当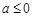 时
时 在
在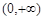 上没有极值点,当
上没有极值点,当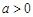 时,
时, 在
在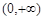 上有一个极小值点.
上有一个极小值点.
(Ⅱ)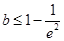 .
.
(Ⅲ)当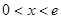 时,
时,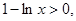 ∴
∴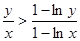 ,
,
当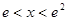 时,
时,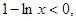 ∴
∴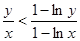
【解析】
试题分析:(Ⅰ)因为函数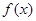 的定义域为
的定义域为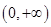 且
且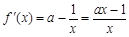 ,
,
故①当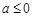 时,
时,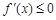 在
在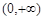 上恒成立,函数
上恒成立,函数 在
在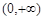 单调递减,此时
单调递减,此时 在
在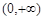 上没有极值点;
上没有极值点;
②当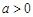 时,由
时,由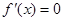 得
得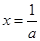 ,由
,由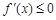 得
得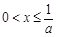 ,由
,由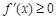 得
得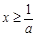 ,
,
∴ 在
在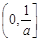 上递减,在
上递减,在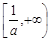 上递增,此时
上递增,此时 在
在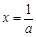 处有极小值.
处有极小值.
综上,当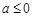 时
时 在
在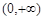 上没有极值点,当
上没有极值点,当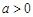 时,
时, 在
在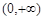 上有一个极小值点.
4分
上有一个极小值点.
4分
(Ⅱ)∵函数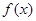 在
在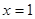 处取得极值,∴
处取得极值,∴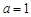 ,
,
∴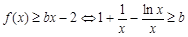 , 6分
, 6分
令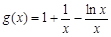 ,可得
,可得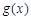 在
在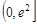 上递减,在
上递减,在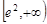 上递增,
上递增,
∴ ,即
,即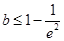 . 9分
. 9分
(Ⅲ)解:令 , 10分
, 10分
由(Ⅱ)可知 在
在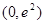 上单调递减,则
上单调递减,则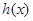 在
在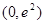 上单调递减
上单调递减
∴当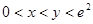 时,
时,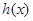 >
>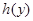 ,即
,即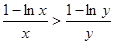 . 11分
. 11分
当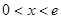 时,
时,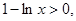 ∴
∴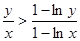 ,
,
当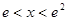 时,
时,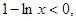 ∴
∴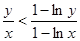 14分
14分
考点:本题主要考查导数的应用,求函数的单调区间、极值、证明不等式。
点评:典型题,在研究函数单调区间、求极值过程中,基本方法步骤是:求导数、求驻点、解不等式、定导数符号,确定函数的单调区间及极值。利用导数证明不等式,应首先构造函数,研究函数的单调性,确定函数与最值的关系。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
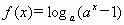 ,(
,(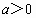 ,
,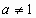 ),
),
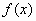 的定义域;
的定义域;
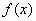 的单调性.
的单调性.