题目内容
(1)试用万能公式证明:tan| α |
| 2 |
| sinα |
| 1+cosα |
(2)已知sinα=
| 4 |
| 5 |
| α |
| 2 |
分析:(1)根据万能公式可用tan
分别表示出sinα和cosα,进而可求1+cosα,代入
结果正好为tan
原式得证.
(2)利用同角三角函数基本关系求得cosα的值,进而根据(1)中的结论求得tan
的值.
| α |
| 2 |
| sinα |
| 1+cosα |
| α |
| 2 |
(2)利用同角三角函数基本关系求得cosα的值,进而根据(1)中的结论求得tan
| α |
| 2 |
解答:解:(1)证明:由sinα=
及cosα=
得1+cosα=
故tan
=
.
(2)解:由sinα=
,α为第二象限角得cosα=-
由(1)得tan
=
=
=2.
2tan
| ||
1+tan2
|
1-tan2
| ||
1+tan2
|
| 2 | ||
1+tan2
|
故tan
| α |
| 2 |
| sinα |
| 1+cosα |
(2)解:由sinα=
| 4 |
| 5 |
| 3 |
| 5 |
由(1)得tan
| α |
| 2 |
| sinα |
| 1+cosα |
| ||
1-
|
点评:本题主要考查了三角函数恒等式的证明,同角三角函数基本关系的应用,万能公式的运用.考查了学生对三角函数基础知识的把握.

练习册系列答案
相关题目
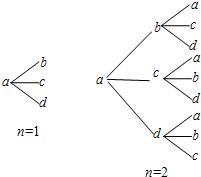 用a,b,c,d四个不同字母组成一个含n+1(n∈N+)个字母的字符串,要求由a开始,相邻两个字母不同.例如n=1时,排出的字符串是ab,ac,ad;n=2时排出的字符串是aba,abc,abd,aca,acb,acd,ada,adb,adc,…,如图所示.记这含n+1个字母的所有字符串中,排在最后一个的字母仍是a的字符串的种数为an.
用a,b,c,d四个不同字母组成一个含n+1(n∈N+)个字母的字符串,要求由a开始,相邻两个字母不同.例如n=1时,排出的字符串是ab,ac,ad;n=2时排出的字符串是aba,abc,abd,aca,acb,acd,ada,adb,adc,…,如图所示.记这含n+1个字母的所有字符串中,排在最后一个的字母仍是a的字符串的种数为an.