题目内容
如图,三棱锥D—ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.
(1)求证:平面CDE⊥平面ABD;
(2)求直线AD和平面CDE所成的角的大小;
(3)求点A到平面BCD的距离.
(1)证明:∵AD⊥平面ABC,CE![]() 平面ABC,
平面ABC,
∴AD⊥CE.
又∵△ABC为正三角形,E为AB的中点,
∴CE⊥AB.而AB∩AD=A,
∴CE⊥平面ABD.
又CE![]() 平面CDE,∴平面CDE⊥平面ABD.
平面CDE,∴平面CDE⊥平面ABD.
(2)解:由(1)得平面CDE⊥平面ABD,
∴AD在平面CDE上的射影在DE上.
∴∠ADE即为所成的角.
△ADE为直角三角形,且AE=2,AD=3,
∴tan∠ADE=![]() .
.
∴∠ADE=arctan![]() ,
,
即直线AD与平面CDE所成的角为arctan![]() .
.
(3)解:设点A到平面BCD的距离为h,
则有V==VA—BCD,即![]() ×S△ABC×AD=
×S△ABC×AD=![]() ×S△BCD×h.
×S△BCD×h.
又∵S△ABC=4![]() ,AD=3,S△BCD=2
,AD=3,S△BCD=2![]() .
.
解得h=![]() .
.

练习册系列答案
相关题目
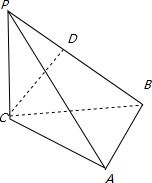 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB. 如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.
如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.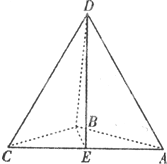 如图,三棱锥D-ABC中,AB,BC,BD两两垂直,且AB=BC=2,点E是AC中点,异面直线AD与BE所成角为θ.
如图,三棱锥D-ABC中,AB,BC,BD两两垂直,且AB=BC=2,点E是AC中点,异面直线AD与BE所成角为θ. 如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.
如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.