题目内容
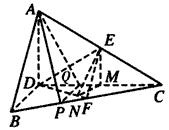
如图所示,正三角形ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角E-DF-C的余弦值;
(3)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论。
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角E-DF-C的余弦值;
(3)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论。
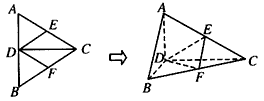
| 解:(1)在△ABC中,E、F分别是AC、BC的中点, ∴EF∥AB, 又AB  平面DEF,EF 平面DEF,EF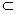 平面DEF, 平面DEF,∴AB∥平面DEF。 |
|
| (2)∵AD⊥CD,BD⊥CD, ∴∠ADB是二面角A-CD-B的平面角, ∴AD⊥BD,AD⊥平面BCD, 如图,取CD的中点M,连接EM,则EM∥AD, ∴EM⊥平面BCD, 过M作MN⊥DF于点N,连接EN,则EN⊥DF, ∴∠MNE是二面角E-DF-C的平面角, 易知,在Rt△EMN中,EM=1, 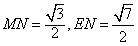 , ,∴ 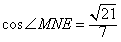 。 。(3)在线段BC上存在点P,使AP⊥DE, 证明如下:如图(甲),在线段BC上取点P,使 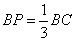 , ,过P点作PQ⊥CD于点Q,连接AQ, ∴PQ⊥平面ACD, ∴PQ⊥DE, 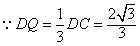 ,且AD=2, ,且AD=2,∴∠DAQ=30°, 又△ADE为等边三角形, ∴AQ⊥DE, 又AQ∩PQ=Q, ∴DE⊥平面APQ, ∵AP  平面APQ, 平面APQ,∴AP⊥DE. |
 |

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
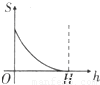
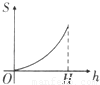
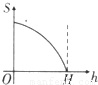
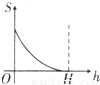
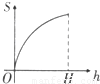
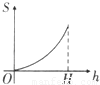
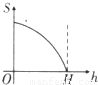
 如图所示,正三角形中阴影部分的面积S是h(0≤h≤H)的函数,则该函数的图象是( )
如图所示,正三角形中阴影部分的面积S是h(0≤h≤H)的函数,则该函数的图象是( )