题目内容
函数 的零点所在的区间为( )
的零点所在的区间为( )
| A.(-1,0) | B.( ,1) ,1) | C.(1,2) | D.(1, ) ) |
B
解析试题分析:令f(x)=x+lnx=0,
可得lnx=-x,再令g(x)=lnx,h(x)=-x,在同一坐标系中画出g(x),h(x)的图象,
可知g(x)与h(x)的交点在(0,1),从而函数f(x)的零点在(0,1),
故选B.
考点:本试题主要考查了函数零点的概念和零点存在性定理的运用,属于基础题。
点评:解决该试题的最简单的方法令函数f(x)=0得到lnx=-x,转化为两个简单函数g(x)=lnx,h(x)=-x,最后在同一坐标系中画出g(x),h(x)的图象,进而可得答案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数 在
在 上是增函数,则
上是增函数,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数 的零点所在的区间是
的零点所在的区间是
A. | B. | C. | D. |
设 ,用二分法求方程
,用二分法求方程 在
在 内近似解的过程中得
内近似解的过程中得 ,则方程的根落在区间( )
,则方程的根落在区间( )
A. | B. | C. | D.不能确定 |
下列四个函数中,在 上为增函数的是( )
上为增函数的是( )
A. | B. | C. | D. |
已知函数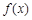 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, 则函数
则函数 =
= 在
在 上的所有零点之和为
上的所有零点之和为
| A.7 | B.8 | C.9 | D.10 |
 用二分法求方程
用二分法求方程 在区间
在区间 上近似解的
上近似解的 ,
, ,则方程的根落在区间( )
,则方程的根落在区间( )




 与奇函数
与奇函数 的定义域都是
的定义域都是 ,它们在
,它们在 上的图象分别为图(1)、(2)所示,则使关于
上的图象分别为图(1)、(2)所示,则使关于 的不等式
的不等式 成立的
成立的



