题目内容
设m、n为垂直的异面直线，α、β是两个不同的平面，下列命题正确的是
- A.如果m⊥α，n⊥β，那么α∥β
- B.如果m∥α，n∥β，那么α∥β
- C.如果m⊥α，n∥β，那么α⊥β
- D.如果m⊥α，n⊥β，那么α⊥β
D
分析：m、n为垂直的异面直线，α、β是两个不同的平面：如果m⊥α，n⊥β，那么α⊥β；如果m∥α，n∥β，那么α∥β或α与β相交；如果m⊥α，n∥β，那么α∥β或α与β相交．
解答：m、n为垂直的异面直线，α、β是两个不同的平面：
如果m⊥α，n⊥β，那么α⊥β，故A不成立，D成立；
如果m∥α，n∥β，那么α∥β或α与β相交，故B不成立；
如果m⊥α，n∥β，那么α∥β或α与β相交，故C不成立．
故选D．
点评：本题考查平面的基本性质及推论，是基础题．解题时要认真审题，仔细解答．
分析：m、n为垂直的异面直线，α、β是两个不同的平面：如果m⊥α，n⊥β，那么α⊥β；如果m∥α，n∥β，那么α∥β或α与β相交；如果m⊥α，n∥β，那么α∥β或α与β相交．
解答：m、n为垂直的异面直线，α、β是两个不同的平面：
如果m⊥α，n⊥β，那么α⊥β，故A不成立，D成立；
如果m∥α，n∥β，那么α∥β或α与β相交，故B不成立；
如果m⊥α，n∥β，那么α∥β或α与β相交，故C不成立．
故选D．
点评：本题考查平面的基本性质及推论，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
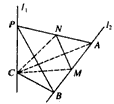
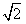（2010•福建模拟）如图，l1、l2是两条互相垂直的异面直线，点P、C在直线l1上，点A、B在直线l2上，M、N分别是线段AB、AP的中点，且PC=AC=a，
a，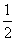
AB；②AB=
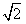a；③CM⊥AB；④BC⊥AC。请你从中再选择两个条件以确定cosθ的值，并求解． 