题目内容
已知△ABC的三个顶点在抛物线 :x2=y上运动.
:x2=y上运动.(1)求
 的焦点坐标;
的焦点坐标;(2)若点A在坐标原点,且∠BAC=
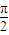 ,点M在BC上,且
,点M在BC上,且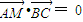 ,求点M的轨迹方程;
,求点M的轨迹方程;(3)试研究:是否存在一条边所在直线的斜率为
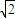 的正三角形ABC,若存在,求出这个正三角形ABC的边长,若不存在,说明理由.
的正三角形ABC,若存在,求出这个正三角形ABC的边长,若不存在,说明理由.
【答案】分析:(1)由抛物线的方程,可得抛物线的焦点在y轴上,开口向上,故可得焦点坐标;
(2)设点M的坐标为(x,y),设出AB、AC方程与抛物线方程联立,确定B、C的坐标,从而可得BC的方程,利用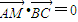 ,即可求得点M的轨迹方程;
,即可求得点M的轨迹方程;
(3)设A、B、C的坐标,求得△ABC的三边所在直线的斜率,若AB边所在直线的斜率为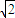 ,AB边所在直线和x轴的正方向所成角为α(0°<α<90°),则tanα=
,AB边所在直线和x轴的正方向所成角为α(0°<α<90°),则tanα=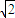 ,得出坐标之间的关系,即可求得|AB|.
,得出坐标之间的关系,即可求得|AB|.
解答:解:(1)由x2=y可得焦点在y轴的正半轴上,且2p=1,所以,焦点坐标为(0, ) …(3分)
) …(3分)
(2)设点M的坐标为(x,y),AB方程为y=kx,由∠BAC=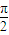 得AC方程为y=-
得AC方程为y=-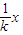 ,则
,则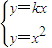 得B(k,k2),同理可得C(-
得B(k,k2),同理可得C(-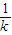 ,
,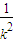 )
)
∴BC方程为y-k2=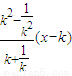 恒过定点P(0,1),…(10分)
恒过定点P(0,1),…(10分)
∴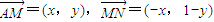
∵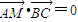
∴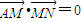 ,
,
所以,-x×x+y(1-y)=0,即y2+x2-y=0(x≠0)
(3)设A(p,p2),B(q,q2),C(r,r2),△ABC的三边所在直线AB,BC,CA的斜率分别是p+q,q+r,r+p------①…(12分)
若AB边所在直线的斜率为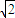 ,AB边所在直线和x轴的正方向所成角为α(0°<α<90°),则tanα=
,AB边所在直线和x轴的正方向所成角为α(0°<α<90°),则tanα=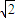 ,
,
所以 …(14分)
…(14分)
∴q-p=tan(α-60°)-tan(α+60°)=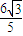 -----②
-----②
又p+q=tanα=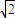 --------------③…(16分)
--------------③…(16分)
所以,|AB|=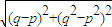 =
=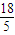 …(18分)
…(18分)
点评:本题考查抛物线的性质,考查轨迹方程的求解,考查向量知识的运用,考查直线的斜率的计算,综合性强.
(2)设点M的坐标为(x,y),设出AB、AC方程与抛物线方程联立,确定B、C的坐标,从而可得BC的方程,利用
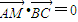 ,即可求得点M的轨迹方程;
,即可求得点M的轨迹方程;(3)设A、B、C的坐标,求得△ABC的三边所在直线的斜率,若AB边所在直线的斜率为
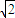 ,AB边所在直线和x轴的正方向所成角为α(0°<α<90°),则tanα=
,AB边所在直线和x轴的正方向所成角为α(0°<α<90°),则tanα=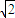 ,得出坐标之间的关系,即可求得|AB|.
,得出坐标之间的关系,即可求得|AB|.解答:解:(1)由x2=y可得焦点在y轴的正半轴上,且2p=1,所以,焦点坐标为(0,
 ) …(3分)
) …(3分)(2)设点M的坐标为(x,y),AB方程为y=kx,由∠BAC=
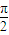 得AC方程为y=-
得AC方程为y=-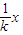 ,则
,则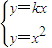 得B(k,k2),同理可得C(-
得B(k,k2),同理可得C(-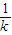 ,
,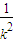 )
)∴BC方程为y-k2=
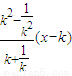 恒过定点P(0,1),…(10分)
恒过定点P(0,1),…(10分)∴
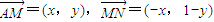
∵
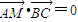
∴
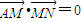 ,
,所以,-x×x+y(1-y)=0,即y2+x2-y=0(x≠0)
(3)设A(p,p2),B(q,q2),C(r,r2),△ABC的三边所在直线AB,BC,CA的斜率分别是p+q,q+r,r+p------①…(12分)
若AB边所在直线的斜率为
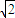 ,AB边所在直线和x轴的正方向所成角为α(0°<α<90°),则tanα=
,AB边所在直线和x轴的正方向所成角为α(0°<α<90°),则tanα=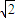 ,
,所以
 …(14分)
…(14分)∴q-p=tan(α-60°)-tan(α+60°)=
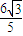 -----②
-----②又p+q=tanα=
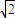 --------------③…(16分)
--------------③…(16分)所以,|AB|=
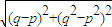 =
=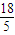 …(18分)
…(18分)点评:本题考查抛物线的性质,考查轨迹方程的求解,考查向量知识的运用,考查直线的斜率的计算,综合性强.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
已知△ABC的三个顶点在半径为1的球面上,且AB=1,BC=
.若A、C两点的球面距离为
,则球心O到平面ABC的距离为( )
| 3 |
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|