题目内容
已知圆面C:(x-a)2+y2≤a2-1的面积为S,平面区域D:2x+y≤4与圆面C的公共区域的面积大于
S,则实数a的取值范围是( )
| 1 |
| 2 |
| A、(-∞,2) |
| B、(-∞,2] |
| C、(-∞,-1)∪(1,2) |
| D、(-∞,-1)∪(1,2] |
分析:由题意:“平面区域D:2x+y≤4与圆面C的公共区域的面积大于
S”结合圆的对称性得,圆面C:(x-a)2+y2≤a2-1的圆心(a,0)在平面区域:2x+y<4内即可,从而列出不等关系即可解得实数a的取值范围.
| 1 |
| 2 |
解答:解:由题意得:
圆面C:(x-a)2+y2≤a2-1的圆心(a,0)在平面区域:2x+y<4内,
则
?a∈(-∞,-1)∪(1,2).
故选C.
圆面C:(x-a)2+y2≤a2-1的圆心(a,0)在平面区域:2x+y<4内,
则
|
故选C.
点评:本小题主要考查简单线性规划的应用、直线与圆的位置关系、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则实数a的取值范围是
,则实数a的取值范围是 ,则实数a的取值范围是( )
,则实数a的取值范围是( )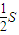 ,则实数a的取值范围是( )
,则实数a的取值范围是( )